Обратная матрица

Определение. Матрицей, обратной квадратной матрице A, называется квадратная матрица B, удовлетворяющая равенствам

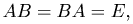
где E - единичная матрица.

Из определения следует, что обратная матрица существует только для квадратной матрицы и обе матрицы имеют один и тот же порядок. Матрицу, обратную матрице A, обозначают A^-1.

Рассмотрим квадратную матрицу n-го порядка:

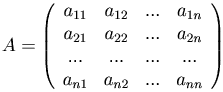
Матрицей, присоединенной к матрице A, называется матрица

где A_ik - алгебраическое дополнение элемента a_ik матрицы A. Причем алгебраические дополнения элементов i-й строки матрицы A расположены в i-м столбце матрицы C.

Теорема. Если A - квадратная матрица порядка n, а C - присоединенная к ней матрица, то

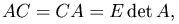
где E - единичная матрица n-го порядка.

Квадратная матрица называется невырожденной, или неособенной, если определитель ее отличен от нуля. Если определитель матрицы равен нулю, то матрица называется вырожденной, или особенной.

Теорема. Для невырожденной матрицы A существует единственная обратная матрица A^-1, определяемая формулой

где C - матрица, присоединенная к матрице A.

Свойства невырожденных матриц:

;
(A^-1)^-1=A;
(AB)^-1=B^-1A^-1.

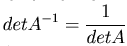Замечание. Вырожденная матрица не имеет обратной.

Матричное представление систем линейных уравнений

Рассмотрим систему n линейных уравнений с n неизвестными x₁, x₂, …, x_n

где a_ij, b_i (i, j = 1, … n) - числа.

Рассмотрим основную матрицу системы (составленную из коэффициентов линейных уравнений системы):

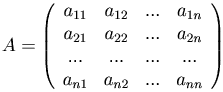
и матрицы-столбцы, составленные из неизвестных и свободных членов соответственно:

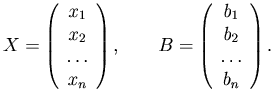
Тогда линейную систему можно представить в матричной форме:

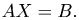
В случае, если определитель матрицы A отличен от нуля, эта матрица имеет обратную. Умножим обе части последней формулы на матрицу A^-1 слева:

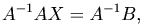
получим решение системы с помощью обратной матрицы:

Правило Крамера

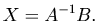
Теорема. Система n линейных уравнений с n неизвестными, определитель Δ которой отличен от нуля, обладает решением, и притом только одним. Решение находится по правилу Крамера:

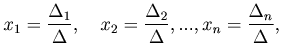
где Δ_i (i=1, …, n) - определитель, полученный из определителя Δ заменой его i-го столбца столбцом из свободных членов.