Матрицы

Определение. Матрицей называется прямоугольная таблица, состоящая из m строк и n столбцов, записанная в виде:

Числа этой таблицы a_ik называются элементами матрицы. Для любого элемента a_ik первый индекс i обозначает номер строки, а второй индекс k - номер столбца. Матрицу, имеющую m строк и n столбцов называют матрицей размера m×n. Краткие обозначения такой матрицы:

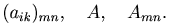
Определение. Две матрицы A_mn=(a_ik)_mn, B_pq=(b_ik)_pq называются равными, если p=m, q=n и a_ik=b_ik (i=1,2,…,m; k=1,2,…,n).

Другими словами, если они одинаковых размеров и их соответствующие элементы равны.

Матрица, состоящая из одной строки (a₁₁, a₁₂, … , a_1n) называется матрицей-строкой.

Матрица, состоящая из одного столбца 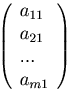называется матрицей-столбцом.

Матрица, все элементы которой равны нулю, называется нулевой матрицей:

Если число строк у матрицы не равно числу столбцов (m≠n), то матрица называется прямоугольной, иначе - квадратной. Число строк (или столбцов) квадратной матрицы называется ее порядком. Диагональ квадратной матрицы, содержащая элементы a₁₁, a₂₂, …, a_nn, называется главной, а диагональ, которая содержит элементы a_1n, a_{2, n-1}, …, a_n1 - побочной (или вспомогательной, или второй).

Диагональной матрицей называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю, то есть матрица

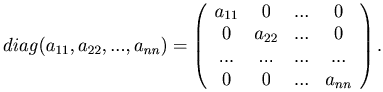
Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны единице:

Краткое обозначение единичной матрицы: E = (δ_ik), где δ_ik - символ Кронекера, то есть

Линейные действия над матрицами

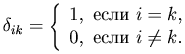
Линейными действиями над матрицами называются сложение и вычитание матриц, умножение матрицы на число. Сложение и вычитание матриц определяется только для матриц одинаковых размеров.

Суммой двух матриц A=(a_ik)_mn, B=(b_ik)_mn называется такая матрица C=(c_ik)_mn, что

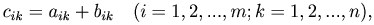
то есть матрица, элементы которой равны суммам соответствующих элементов матриц слагаемых. Сумма двух матриц A и B обозначается A+B.

Разностью A-B двух матриц A=(a_ik)_mn, B=(b_ik)_mn называется такая матрица D=(d_ik)_mn, что

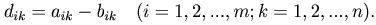
Произведением матрицы A=(a_ik)_mn на число α (или числа α на матрицу A) называется матрица B=(b_ik)_mn, для которой

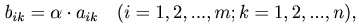
то есть матрица, полученная из данной умножением всех ее элементов на число α. Произведением матрицы A на число α обозначаетсяα A или A α.

Матрицу (-1)A будем называть матрицей, противоположной матрице A, и обозначать -A.

Свойства линейных операций:

A+B=B+A,
(A+B)+C=A+(B+C),
A+O=A,
A+(-A)=O,
1·A=A,
α(β A)=(αβ)A,
α(A+B)=α A+α B,
(α+β)A=α A+β A,

где A, B, C - матрицы одних и тех же размеров; O - нулевая матрица; (-A) - матрица, противоположная матрице A; α, β - любые действительные числа.

Умножение матриц

Определение. Матрица A называется согласованной с матрицей B, если число столбцов матрицы A равно числу строк матрицы B, то есть матрица A_mn согласована с матрицей B_nl.

Из согласованности матрицы A с матрицей B не следует согласованность матрицы B с матрицей A. Если A и B - квадратные матрицы одного порядка, то они взаимно согласованы.

Операция умножения матриц определяется только для согласованных матриц.

Определение. Произведением матрицы A_mn=(a_ik)_mn на матрицу B_nl=(b_ik)_nl называется новая матрица C_ml=(c_ik)_ml, у которой элемент c_ik равен сумме произведений элементов i-й строки матрицы A на k-й столбец матрицы B, т.е.

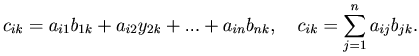
Произведение матрицы A на матрицу B обозначается AB.

Замечание. Так как из согласованности A с B не следует согласованность B с A, то из того, что существует произведение AB не следует, что существует произведение BA.

Пример. Даны две матрицы второго порядка

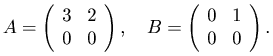
Если найти произведения AB и BA, то из данного примера можем сделать следующие заключения:

В общем случае AB ≠ BA.
Произведение матриц может быть нулевой матрицей, когда оба множителя не являются нулевыми матрицами.

Определение. Если для матриц AB и BA определены произведения AB и BA и AB=BA, то матрицы AB и BA называются перестановочными или коммутативными.

Примеры коммутативных матриц: матрицы E и O с любой матрицей A коммутативны. AE=EA=A, AO=OA=O, то есть при умножении матриц единичная матрица играет роль единицы, а нулевая матрица - роль нуля.

Свойства умножения матриц: если имеют смысл соответствующие действия, то

(AB)C=A(BC) - ассоциативность;
α(AB)=(α A)B=A(α B);
(A+B)C=AC+BC - дистрибутивность;
C(A+B)=CA+CB.

Транспонирование матрицы

Определение. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.

Матрицу, транспонированную относительно матрицы A, обозначают A^T.

Если 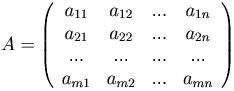, то . Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы.

Свойства транспонирования:

(A^T)^T=A;
(α A)^T=α A^TT;
(A+B)^T=A^T+B^T;
(AB)^T=B^TA^T.

Задачи

Вычислить линейную комбинацию.

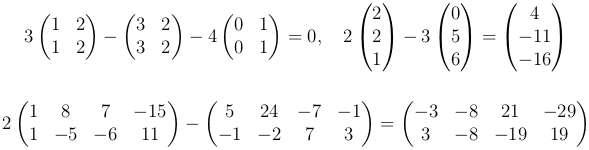
Вычислить произведения матриц.