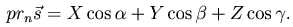Линейная и векторная алгебра
Линейная и векторная алгебра
 Основные понятия векторной алгебры
Основные понятия векторной алгебры
Определение. Вектором называется направленный отрезок.
Обозначения: 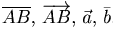 . У вектора
. У вектора 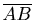 точка A называется началом
вектора, а точка B - конец вектора.
точка A называется началом
вектора, а точка B - конец вектора.
Определение. Модулем вектора называется его длина.
Обозначения: 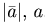 .
.
Определение. Нуль-вектором (или нулевым вектором) называется вектор, начало и конец которого совпадает.
Обозначение: 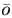 . Модуль нулевого вектора равен нулю, а направление не определено.
. Модуль нулевого вектора равен нулю, а направление не определено.
Определение. Единичным вектором называется вектор, длина которого равна единице.
Определение. Векторы, лежащие на параллельных прямых (или на одной прямой), называются коллинеарными.
Определение. Коллинеарные векторы, имеющие одинаковые направления и равные длины, называются равными.
Из определения равенства векторов следует, что каков бы ни был вектор 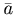 и точка A, всегда можно построить единственный вектор
и точка A, всегда можно построить единственный вектор 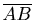 с началом в точке A, равный вектору
с началом в точке A, равный вектору 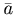 , т.е.
, т.е. 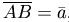 , или, как говорят, перенести вектор
, или, как говорят, перенести вектор 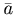 в точку A.
в точку A.
Определение. Векторы, противоположно направленные и имеющие равные длины, называются противоположными.
Обозначение: 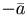 .
.
Определение. Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называются компланарными.
Определение. Суммой 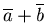 векторов
векторов 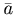 и
и 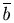 называется вектор, проведенный из начала
называется вектор, проведенный из начала 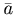 к концу
к концу 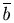 , если конец
, если конец 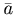 и начало совмещены
и начало совмещены 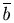 (правило треугольника).
(правило треугольника).
Определение. Суммой n векторов 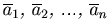 называется вектор, начало которого совпадает с
началом первого вектора
называется вектор, начало которого совпадает с
началом первого вектора 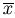 , конец - с концом
последнего
, конец - с концом
последнего 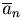 при условии, что каждый последующий
вектор
при условии, что каждый последующий
вектор 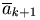 отложен из конца предыдущего
отложен из конца предыдущего 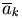 (k=1,…,n) (правило замыкающей).
(k=1,…,n) (правило замыкающей).
Свойства операции сложения:
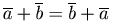 (коммутативность);
(коммутативность);
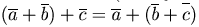 (ассоциативность);
(ассоциативность);
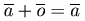 (наличие нулевого
элемента);
(наличие нулевого
элемента);
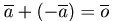 (наличие
противоположного элемента).
(наличие
противоположного элемента).
Определение. Разностью 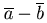 векторов
векторов 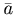 и
и 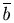 называется вектор
называется вектор 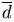 такой, что в сумме с вектором
такой, что в сумме с вектором 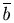 дает вектор
дает вектор 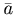 :
:
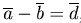 , если
, если
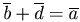
Определение. Произведением 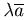 вектора
вектора 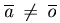 на число λ≠0 называется вектор
на число λ≠0 называется вектор
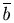 , модуль которого
, модуль которого 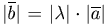 и который направлен в ту же сторону, что и вектор
и который направлен в ту же сторону, что и вектор 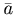 , если λ>0, и противоположную, если λ<0. Если λ=0 и/или
, если λ>0, и противоположную, если λ<0. Если λ=0 и/или
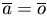 , то
, то
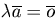 .
.
Свойства произведения вектора на число::
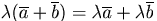 (дистрибутивность относительно сложения
векторов);
(дистрибутивность относительно сложения
векторов);
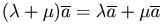 (дистрибутивность относительно сложения двух
чисел);
(дистрибутивность относительно сложения двух
чисел);
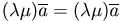 (ассоциативность);
(ассоциативность);
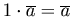 (умножение на единицу).
(умножение на единицу).
Теорема [Необходимое и достаточное условие коллинеарности двух векторов]. Вектора 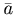 и
и 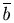 коллинеарны, если выполняется следующее равенство:
коллинеарны, если выполняется следующее равенство:
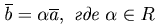
Рассмотрим некоторый вектор 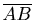 и ось l. Пусть точки A1 и B1 - точки пересечения оси l с перпендикулярными ей плоскостями, проходящими через точки A и B.
и ось l. Пусть точки A1 и B1 - точки пересечения оси l с перпендикулярными ей плоскостями, проходящими через точки A и B.
Определение. Проекцией вектора 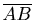 на ось l называется число, равное длине вектора
на ось l называется число, равное длине вектора 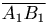 , взятой со знаком "плюс", если направление вектора
, взятой со знаком "плюс", если направление вектора 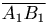 совпадает с направлением оси и со знаком "минус" в противном случае.
совпадает с направлением оси и со знаком "минус" в противном случае.
Обозначение: 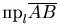 .
.
Проекция вычисляется по формуле:
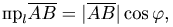
где ϕ - угол между вектором 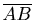 и осью l.
и осью l.
Основные свойства проекции:
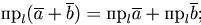
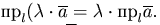
Если 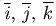 - орты координатных осей прямоугольной системы координат Oxyz, то любой вектор
- орты координатных осей прямоугольной системы координат Oxyz, то любой вектор 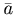 единственным образом можно представить в виде их суммы, т.е. линейной комбинации, с коэффициентами
единственным образом можно представить в виде их суммы, т.е. линейной комбинации, с коэффициентами 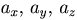 :
:
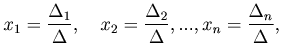
Коэффициенты 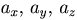 линейной комбинации называют координатами вектора
линейной комбинации называют координатами вектора 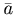 в базисе
в базисе 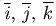 . Координаты
. Координаты 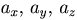 вектора
вектора 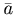 - это его проекции на координатные оси. Запись:
- это его проекции на координатные оси. Запись:
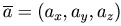
Длина вектора определяется по формуле:
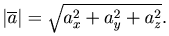
Вектор 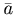 образует с координатными осями Ox, Oy, Oz углы α, β, γ соответственно. Направление этого вектора определяется с помощью направляющих косинусов, для которых справедливы равенства:
образует с координатными осями Ox, Oy, Oz углы α, β, γ соответственно. Направление этого вектора определяется с помощью направляющих косинусов, для которых справедливы равенства:
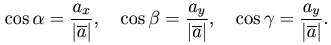
Направляющие косинусы связаны соотношением: 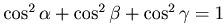 .
.
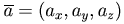 и
и 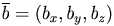 .
.
1) Необходимое и достаточное условие коллинеарности векторов можно записать как
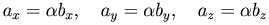
Если ни одна из координат второго вектора не обращается в нуль, то
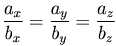
Т.е. векторы коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.
2) 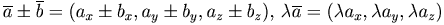 .
.
3) Пусть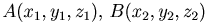 , тогда
, тогда
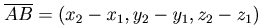 4) Пусть заданы n векторов
4) Пусть заданы n векторов 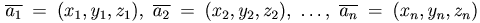 и их линейная комбинация
и их линейная комбинация
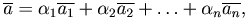
тогда
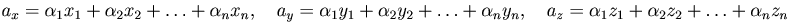
Определение. Скалярным произведением 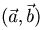 ненулевых векторов
ненулевых векторов 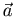 и
и 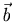 называется произведение их модулей на косинус угла ϕ между ними:
называется произведение их модулей на косинус угла ϕ между ними:
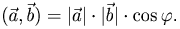
Скалярное произведение обозначается также 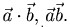
Так как 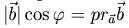 (
(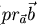 - проекция вектора
- проекция вектора 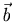 на вектор
на вектор 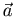 ) и $|
) и $|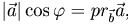 , то можем
записать
, то можем
записать
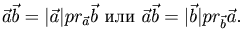
Понятие скалярного произведения возникло в механике. Если вектор 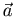 изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора 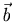 , то работа этой силы определяется равенством
, то работа этой силы определяется равенством 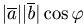 .
.
Необходимое и достаточное условие перпендикулярности двух векторов: Вектора 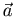 и
и 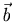 перпендикулярны тогда и только тогда, когда выполняется равенство
перпендикулярны тогда и только тогда, когда выполняется равенство 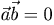 .
.
Свойства скалярного произведения:
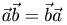 (коммутативность);
(коммутативность);
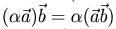 (ассоциативность);
(ассоциативность);
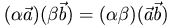 ;
;
 (дистрибутивность относительно суммы векторов).
(дистрибутивность относительно суммы векторов).
Пример. 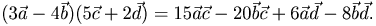
Теорема. Скалярное произведение двух векторов
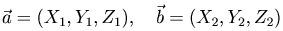
выражается формулой
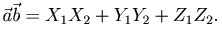
Замечание. Если 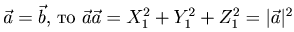 , следовательно,
, следовательно,
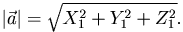
Следствие. Косинус угла φ между векторами 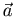 и
и 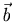 определяется формулой
определяется формулой
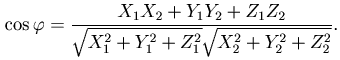
Следствие. Необходимое и достаточное условие перпендикулярности двух векторов выражается равенством
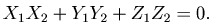
Следствие. Если ось n образует с координатными осями углы α, β, γ соответственно, то проекция вектора 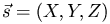 на эту ось определяется равенством
на эту ось определяется равенством