Многомерное векторное пространство

Упорядоченная система n чисел 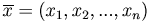называется n-мерным вектором. Каждое число x_i называется i-той координатой или компонентой вектора .

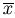Примеры векторов: а) векторы-отрезки, выходящие из начала координат на плоскости или в трехмерном пространстве, будут при фиксированной системе координат соответственно двух- и трехмерными векторами; б) коэффициенты всякого линейного уравнения с n неизвестными составляет n-мерный вектор; в) если дана матрица из m строк и n столбцов, то ее строки будут n-мерными векторами, а столбцы - m-мерными векторами.

Пусть даны два вектора

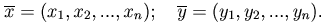
Векторы 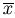и 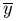будут считаться равными, если равны их соответствующие координаты, т.е. x_i=y_i при i=1, …, n.

Введем операции над векторами:

1) Сложение. Суммой двух векторов называется вектор

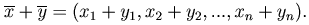
Роль нуля играет нулевой вектор

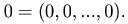
Вектором, противоположным вектору 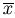назовем вектор

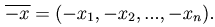
2) Разность. Разностью двух векторов будет вектор

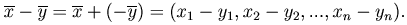
3) Умножение на действительное число. Произведением вектора 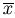на действительное число α называется вектор

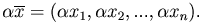
Определение. Совокупность всех n-мерных векторов с действительными компонентами, рассматриваемая с определенными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным векторным пространством.

Линейная зависимость векторов

Определение. Вектор 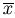называется линейной комбинацией векторов 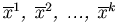, если существуют такие числа 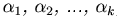, что

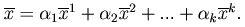
Определение. Система векторов 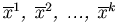называется линейно зависимой, если существуют такие числа 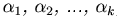, хотя бы одно из которых отлично от нуля, что имеет место равенство

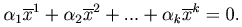
Если это равенство выполняется тогда и только тогда, когда α₁=α₂=…=α_k=0, то такие векторы называются линейно независимыми.

Теорема. Если некоторая подсистема системы векторов является линейно зависимой, то и вся система векторов является линейно зависимой.

Следствие. Если система векторов содержит нулевой вектор, то она линейно зависима.

Следствие. Любая подсистема линейно независимой системы векторов является линейно независимой.

Теорема. Чтобы векторы 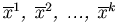(k > 1) были линейно зависимы, необходимо и достаточно, чтобы по меньшей мере один из них был линейной комбинацией остальных.

Теорема(). Пусть 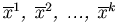- линейно независимая система векторов и 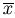- некоторый вектор, тогда система векторов 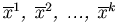, 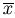является линейно зависимой тогда и только тогда, когда 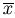- линейная комбинация векторов .

Базис в векторном пространстве

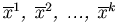Определение. Назовем линейно независимую систему n-мерных векторов 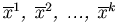максимальной линейно независимой системой, если добавление к этой системе любого n-мерного вектора 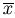дает уже линейно зависимую систему векторов.

Определение. Базисом n-мерного векторного пространства называется максимальная линейно независимая система векторов в этом пространстве.

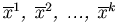Применяя теорему () получаем, что линейно независимая система векторов является базисом пространства тогда и только тогда, когда любой вектор 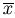из этого пространства является некоторой линейной комбинацией векторов .

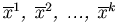Пример базиса n-мерного векторного пространства: набор векторов e₁=(1,0,…,0), e₂=(0,1,…,0), …, e_n=(0,0,…,1) является базисом в Rⁿ.

В каждом ненулевом пространстве имеется бесконечно много базисов.

Другое определение ранга матрицы

Пусть 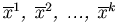- система векторов в Rⁿ.

Определение. Рангом данной системы векторов называется максимальное число линейно независимых векторов в этой системе.

В частности, ранг (или размерность) векторного пространства равен числу элементов базиса этого пространства. Размерность или ранг n-мерного векторного пространства Rⁿ равен n.

Рассмотрим прямоугольную матрицу размера m×n

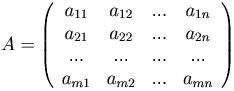
Столбцы этой матрицы, рассматриваемые как m-мерные векторы, могут, вообще говоря, быть линейно зависимыми.

Определение. Рангом матрицы rank(A) называется ранг системы векторов ее столбцов.

Теорема [о базисном миноре]. Базисные строки (базисные столбцы) линейно независимы. Любая строка (столбец) матрицы A является линейной комбинацией базисных строк (базисных столбцов).

Замечание. Теорема о базисном миноре означает, что порядок базисного минора матрицы A равен рангу этой матрицы.

Следствие. Для того, чтобы определитель n-го порядка Δ был равен нулю необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.

Построение решений СЛУ

Пусть рассматривается произвольная система m уравнений с n неизвестными и пусть rang A = r.

Не ограничивая общности, будем считать, что базисный минор матрицы A расположен в левом верхнем углу. Обозначим этот минор:

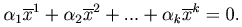
Минор Δ является базисным и для матрицы 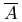, поэтому строки матрицы 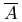с номерами r+1, …, m являются линейными комбинациями первых r ее строк (теорема о базисном миноре). Это означает, что уравнения с номерами r+1, …, m представляют собой линейные комбинации первых r уравнений, так что исходная система эквивалентна системе

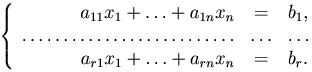
Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор Δ, остальные перенесем вправо

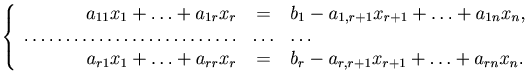
Определение. Неизвестные x₁, …, x_r называются базисными, а переменные x_r+1, …, r_n - свободными.

Свободным переменным можно придавать произвольные значения. Тогда базисные неизвестные определяются по формулам Крамера:

По свойствам определителя:

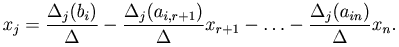
Обозначим 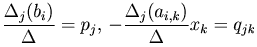. Тогда имеем

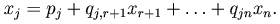
Добавляя сюда очевидные равенства: 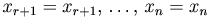, имеем

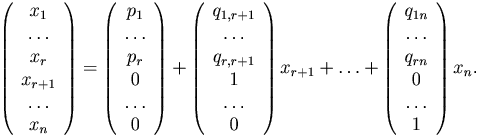
Эти формулы дают общее решение системы.

Теорема [о множестве решений системы однородных уравнений]. Множество решений СОЛУ образует пространство размерности n-r, где r=rang A.

Определение. Всякая линейно независимая система n-r решений системы линейных однородных уравнений называется фундаментальной системой решений.

Таким образом, для того чтобы решить СЛОУ, надо найти фундаментальную систему решений.

Пример.

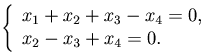
Фундаментальная система решений: E₁(1,0)=(-2,1,1,0)^T, E₂(0,1)=(2,-1,0,1)^T. Общее решение: X=α₁E₁+α₂E₂.