Правые и левые тройки векторов

Определение. Три некомпланарных вектора 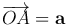, , 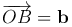, 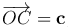взятых в указанном порядке и приложенных в одной точке, называют тройкой векторов a, b, c.

Будем смотреть с конца вектора c на плоскость, определяемую векторами a и b. Если кратчайший поворот от вектора a к вектору b совершается против часовой стрелки, то тройка векторов a, b, c называется правой, если указанный поворот совершается по часовой стрелке, тройка a, b, c называется левой. Все правые (или левые) тройки векторов называются одинаково ориентированными. Если одна тройка является правой, а другая -- левой, то они называются тройками различной ориентации. Если даны три некомпланарных вектора a, b и c, то они образуют 6 троек: a, b, c; b, c; a; c, a, b имеющие одну ориентацию (круговая перестановка векторов), а b, a, c; a, c, b; c, b, a имеют другую ориентацию (перестановка двух векторов).

Определение. Декартова прямоугольная система координат называется правой, если тройка базисных векторов i, j, k является правой и называется левой, если эта тройка левая. В дальнейшем будем рассматривать только правые системы координат.

Векторное произведение векторов

Определение. Векторным произведение вектора a на вектор b называется третий вектор [a, b], удовлетворяющий следующим условиям:

1) |[a, b]|=|a| |b|sin φ, где φ — угол между векторами a и b;
2) вектор [a, b] перпендикулярен каждому из векторов a и b;
3) тройка (a, b, [a, b]) является правой тройкой.

Векторное произведение обозначают также a×b.

Из условия 1) определения следует, что

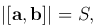
где S — площадь параллелограмма, построенного на векторах a и b. Тогда

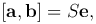
где e — единичный вектор направления вектора [a, b].

Необходимое и достаточное условие коллинеарности двух векторов. Вектора a и b коллинеарны тогда и только тогда, когда

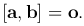
Доказательство. □ Если вектора a и b коллинеарны, то φ=0 или φ=π, тогда sin φ=0, следовательно, |[a, b]|=0, а значит [a, b]=o.

Обратно, если выполнено равенство [a, b]=0 и a≠0, b≠0, то φ=0 или φ=π, следовательно, вектора a и b коллинеарны. ■

Свойства векторного произведения

1. [a, b]=-[b, a] (антикоммутативность);
2. [αa, b]=α[a, b], [a, βb]=β[a, b] (ассоциативность относительно умножения на число);
3. [a+b, c]=[a, c]+[b, c], [a, b+c]=[a, b]+[a, c] (дистрибутивность относительно сложения векторов).

Теорема.Векторное произведение двух векторов a=(X₁, Y₁, Z₁), b=(X₂, Y₂, Z₂) выражается формулой

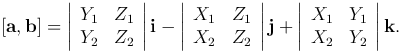
Доказательство. □ Поскольку [i, i] = [j, j] = [k, k]=0, [i, j]=k, [j, k]=i, [k, i]=j, [i, k]=-j, [j, i]=-k, [k, j]=-i, то [a, b]=... ■

Замечание. Эту формулу можно выразить через символический определитель третьего порядка:

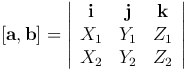
Следствие. Площадь параллелограмма, построенного на векторах a и b, вычисляется по формуле

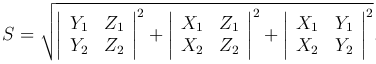
Следствие. Площадь треугольника ABC определяется формулой:

Смешанное произведение векторов

Рассмотрим три вектора a, b, c. Вектор a умножим векторно на b, затем векторное произведение [a, b] умножим скалярно на c. В результате получим число, которое называется смешанным произведением [a, b]c трех векторов a, b, c.

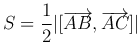
Теорема [геометрический смысл смешанного произведения]. Смешанное произведение [a, b]c трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах 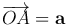, , 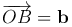, 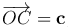взятому со знаком плюс, если тройка (a, b, c) — правая, со знаком минус, если эта тройка — левая.

Доказательство. □Рассмотрим параллелограмм, построенный на векторах 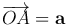, , 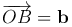лежащих в основании указанного параллелепипеда. Его площадь S=|[a,b]|, тогда можем написать [a, b]=Se, следовательно, [a, b]c=(Se)c=S(ec). Найдем ec = |e| pr_ec = pr_ec. С другой стороны pr_ec=±h, где h — высота параллелепипеда, опущенная на основание OADB. Знак плюс получается, если (a, b, c) — правая тройка, знак минус, если эта тройка левая. Тогда

■

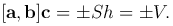Отметим, что V=mod([a, b, c).

Следствие. Векторы a, b, c компланарны тогда и только тогда, когда их смешанное произведение равно нулю, то есть

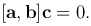
Следствие. Справедливо равенство

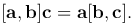
Доказательство. □ Имеем a[b, c]=[b, c]a. По этой теореме [a, b]c=±V, [b, c]a=±V, так как имеем один и тот же параллелепипед. Тройки (a, b, c) и (b, c, a) одной ориентации, значит берем один и тот же знак, следовательно, [a, b]c=[b, c]a=a[b, c]. ■

Замечание 1. Так как верно это следствие, то смешанное произведение обозначают abc.

Замечание 2. Для трех векторов a, b, c имеем

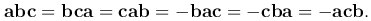
Теорема. Смешанное произведение трех векторов

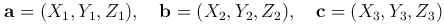
выражается формулой

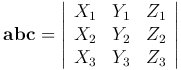
Доказательство. □ Так как abc=[a, b]c, то получим

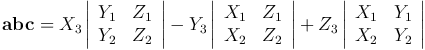
— это разложение определителя третьего порядка по элементам третьей строки. ■

Следствие [Необходимое и достаточное условие компланарности трех векторов]. Три вектора a, b, c компланарны тогда и только тогда, когда выполняется