Классификация дифференциальных уравнений в частных производных второго порядка

Определение. Дифференциальное уравнение второго порядка в частных производных для двух независимых переменных x и y записывают в общем случае соотношением

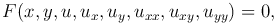
где u=u(x, y) — искомая функция.

Если дифференциальное уравнение линейно относительно старших производных, то его называют квазилинейным уравнением и записывают в виде

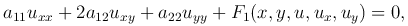(1)

где a₁₁, a₁₂, a₂₂ — некоторые функции независимых переменных.

Дифференциальное уравнение называют линейным, если оно линейно как относительно искомой функции, так и относительно ее частных производных. Такое уравнение записывают в виде

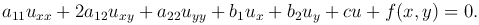(2)

Если коэффициенты этого уравнения не зависят от переменных x и y, то оно представляет собой линейное дифференциальное уравнение с постоянными коэффициентами.

Уравнениям (1), (2) можно поставить в соответствие квадратичную форму

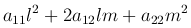
и по аналогии с кривыми второго порядка дать классификацию типов уравнений по знаку дискриминанта.

Определение. Уравнение (1), (2) называются уравнениями гиперболического типа, если в некоторой точке M (или области G) дискриминант уравнения 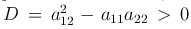, уравнениями параболического типа, если в точке M D = 0, и эллиптического типа, если в точке M D < 0.

Принадлежность уравнения к одному из этих типов определяет некоторые общие свойства его решений и позволяет выбрать методы решения задач такого уравнения.

Уравнения с переменными коэффициентами могут изменять свой тип в различных точках. Примером такого уравнения смешанного типа является уравнение Трикоми

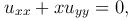
представляющее интерес для газовой динамики. Так как дискриминант этого уравнения D = -x, то уравнение Трикоми является эллиптическим при x > 0 и гиперболическим при x < 0.

В уравнении (1) можно произвести замену независимых переменных

с якобианом преобразования

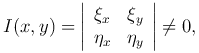
допускающим обратное преобразование. Тогда в новых переменных наше уравнение примет вид

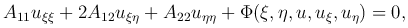(3)

где

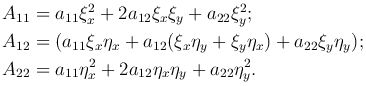
Так как 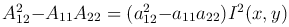, то рассматриваемое преобразование независимых переменных не меняет тип уравнения. Однако функции φ(x, y) и ψ(x, y) можно выбрать такими, чтобы в новых переменных часть коэффициентов обратилась в нуль, а полученное уравнение приняло наиболее простой вид, который называют канонической формой уравнения.

Переход к канонической форме осуществляется с помощью общих интегралов дифференциального уравнения

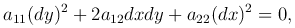
которое называют характеристическим для уравнений (1), (2), а его интегралы — характеристическими кривыми, или характеристиками.

Если φ(x, y) = C — общий интеграл этого характеристического уравнения, то вдоль характеристической кривой имеем

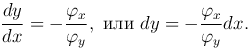
Подставляя это уравнение в характеристическое уравнение, получаем, что функция z = φ(x, y) является решением дифференциального уравнения первого порядка

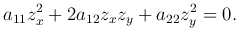(4)

Если в некоторой области G уравнение (1) является уравнением гиперболического типа, то в этой области характеристическое уравнение распадается на два уравнения

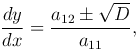
которые имеют два семейства характеристик: φ₁(x, y) = C₁ и φ₂(x, y) = C₂. Тогда с помощью преобразования независимых переменных

приходим к уравнению (3), в котором с учетом (4) A₁₁=0, A₂₂=0. Поэтому, разделив полученное выражение на 2A₁₂≠0, приводим уравнение (3) к канонической форме для уравнений гиперболического типа:

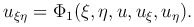
Замечание. Если новые переменные ξ и η имеют вид

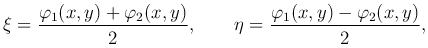
то для уравнения гиперболического типа можно записать вторую каноническую форму

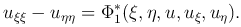
Если в области G уравнение (1) принадлежит к уравнению параболического типа, то в этой области характеристическое уравнение принимает вид

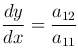
и имеет только одно семейство характеристик: φ(x, y) = C. Тогда, полагая ξ = φ(x, y) и η = ψ(x, y), где ψ — произвольная функция, линейно независимая с функцией φ, приходим к уравнению (3), в котором A₁₁=0. Но так как для уравнения параболического типа 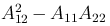, то, следовательно, A₁₂=0. Поэтому после перехода к новым независимым переменным уравнение (3) принимает каноническую форму для уравнений параболического типа:

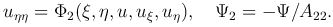
Если в области G уравнение (1) является уравнением эллиптического типа, то характеристическое уравнение приводит к двум уравнениям в комплексной форме

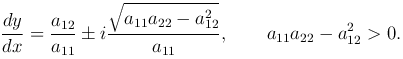
Эти уравнения имеют два комплексно-сопряженных интеграла ρ₁(x,y) = C₁ и ρ₂(x, y) = C₂, где ρ₁(x, y) = φ(x, y) + iψ(x, y), а ρ₂(x, y) = φ(x, y) - iψ(x, y), причем функции φ(x, y) и ψ(x, y) являются действительными функциями своих аргументов.

Функции z₁=ρ₁(x, y) и z₂=ρ₂(x, y) являются решениями уравнения (4) в комплексной области. Поэтому, подставляя их в это уравнение, получим тождество

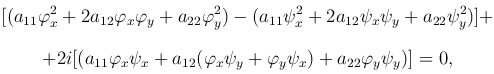
из которого следует, что после преобразования переменных ξ = φ(x, y), η = ψ(x, y) в уравнении (3) A₁₁=A₂₂, а A₁₂=0. Поэтому после преобразования уравнение (3) можно записать в канонической форме для уравнений эллиптического типа: