Уравнение теплопроводности

Рассмотрим одномерный процесс передачи теплоты теплопроводностью в плоском слое изотропного материала, считая, что температура u=u(x, t) является функцией только одного пространственного переменного x.

Обозначим через ρ=ρ(x) плотность материала, c=c(x) — его удельную массовую теплоемкость, k=k(x) — коэффициент теплопроводности.

Предполагаем, что среда неподвижна, а изменение объема материала, связанное с изменением температуры, пренебрежимо мало.

Тогда процесс передачи теплоты в каждой точке пространства описывается дифференциальным уравнением:

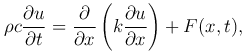
где F(x, t) — объемная плотность тепловых источников.

Для однородного материала с независящими от температуры теплофизическими характеристиками ρ, c и k последнее уравнение можно записать в виде

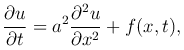
где a² = k/(ρ c) — постоянная, которую называют коэффициентом температуропроводности материала, f(x, t)=F(x, t)/(ρ c). Эти уравнения называются уравнениями теплопроводности. Они являются дифференциальными уравнениями в частных производных параболического типа.

Замечание. Полученные уравнения описывают не только процесс теплопроводности, но и ряд физических процессов диффузионного типа. В частности, диффузионный процесс переноса массы; диффузия частиц в веществе; проникновение магнитного поля в проводящую среду.

Начальные и граничные условия для уравнения теплопроводности

Чтобы с помощью уравнения теплопроводности описать эволюцию температурного поля в теле, необходимо знать распределение температуры в начальный момент времени, то есть задать начальное условие. Для рассматриваемого одномерного процесса начальное условие

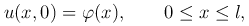
задается в виде известной зависимости φ(x).

Кроме того, требуется знать тепловой режим на поверхности тела S, то есть задать граничные условия во всех точках поверхности тела в любой момент времени. В одномерном процессе граничные условия задаются на граничных поверхностях слоя x=0 и x=l.

Способы задания граничных условий:

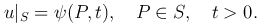
1. Граничное условие первого рода, когда в каждой точке поверхности тела задают температуру

Здесь ψ(P, t) — известная функция точки P поверхности S и времени t.
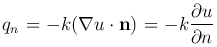2. Граничное условие второго рода, когда на поверхности S тела задают тепловой поток q_n = q·n, где q — вектор плотности теплового потока, n — единичная внешняя нормаль к поверхности S. По закону Фурье . Следовательно, граничное условие второго рода задает на поверхности S нормальную производную температуры и может быть записано в виде

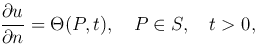
где Θ(P, t) = -q_n/k — известная функция.
В случае теплоизолированной поверхности Θ(P, t)≡0 и мы имеем однородное условие 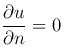на всей поверхности S.
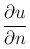3. Граничное условие третьего рода описывает тепловой режим на поверхности тела, соответствующий конвективному теплообмену по закону Ньютона с окружающей внешней средой, имеющей температуру u^{*(P, t)}. Это условие дает связь между температурой u и ее нормальной производной в любой точке поверхности тела

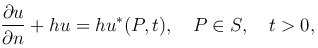
где h=α_T/k, α_T — коэффициент теплообмена.

Замечание. Условия первого, второго и третьего рода можно формально объединить в виде обобщенного граничного условия

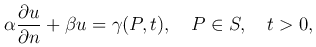
где α и β — некоторые константы, γ(P, t) — заданная на поверхности тела функция.