Краевые задачи для уравнения теплопроводности

Требуется найти решение линейного однородного параболического уравнения

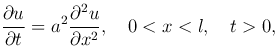(1)

удовлетворяющее при t=0 начальному условию

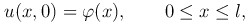(2)

и однородными граничными условиями первого рода

(3)

Используем метод Фурье разделения переменных. Нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (3) ищутся в виде

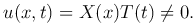
Подставив в уравнение (1) и разделив переменные, получим

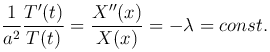
Поэтому функции T(t) и X(x) должны быть определены как решения дифференциальных уравнений

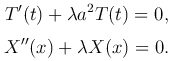
Граничные условия (3) дают условия для функции X(x) в виде

Данная задача имеет нетривиальное решение только при собственных значениях 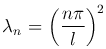, n=1, 2, …, а соответствующие им собственные функции X_n(x) имеют вид

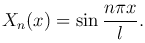
При λ=λ_n для дифференциального уравнения для T запишем общее решение

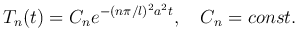
Частные решения уравнения (1), удовлетворяющие граничным условиям (3), имеют вид

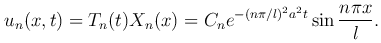
Составим формально ряд

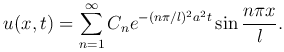(4)

Функция u(x, t) удовлетворяет граничным условиям (3), так как этим условиям удовлетворяет каждый член этого ряда.

Определим коэффициенты C_n так, чтобы выполнялось начальное условие. Подставляя ряд в (2), получим

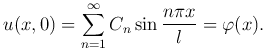
Это соотношение представляет собой разложение функции φ(x) в ряд Фурье по системе ортогональных на отрезке 0≤x≤l собственных функций X_n(x), n=1, 2, …, а коэффициенты C_n являются коэффициентами Фурье и определяются по формуле

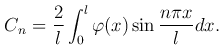(5)

Пусть функция непрерывна на отрезке [0, l] и имеет кусочно--непрерывную производную. Кроме того, пусть φ(0)=φ(l)=0, то есть имеет место согласование начальных и граничных условий. Тогда коэффициенты C_n тригонометрического ряда, определяемые выражением (5), имеют порядок малости O(1/n²). В этом случае числовой ряд 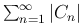сходится и является мажорантным для ряда (4) при t≥0 и 0≤x≤l. Следовательно, ряд (4) сходится к функции u(x, t) равномерно при t≥0, 0≤x≤l, и из непрерывности членов этого ряда вытекает непрерывность суммы u(x, t).