Уравнение Лапласа

Рассмотрим уравнение с частными производными вида

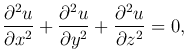
где u=u(x, y, z). Это уравнение называется уравнением Лапласа.

Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:

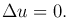
Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.

Неоднородное уравнение

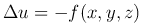
называется уравнением Пуассона.

Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.

Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.

Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.

Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.

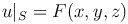
(первая краевая задача), то такая задача называется задачей Дирихле.

Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной

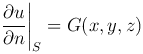
(вторая краевая задача), то такая задача называется задачей Неймана.

Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.

Фундаментальные решения уравнения Лапласа

Рассмотрим уравнение Лапласа

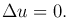
где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно

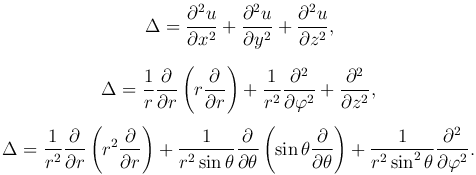
Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.

Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 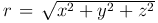точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид

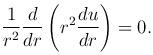
Интегрируя это уравнение, получим

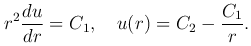
При C₁=-1 и C₂=0 получаем функцию

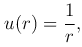
которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.

В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид

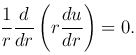
Интегрируя это уравнение, получим

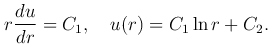
Полагая C₁=-1 и C₂=0, получим

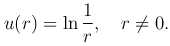
Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.