Решение задачи Дирихле в круге

Рассмотрим внутреннюю краевую задачу для уравнения Лапласа с граничным условием первого рода

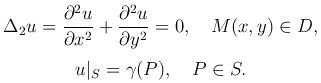
Пусть область D — круг радиуса a, ограниченный окружностью S. Это есть задача Дирихле в круге.

Запишем данную задачу в полярных координатах:

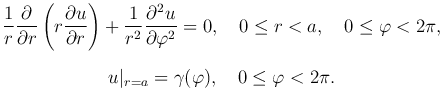
Решение этой задачи будем искать методом разделения переменных в виде

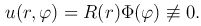
Подставляя это выражение в уравнение Лапласа и разделяя переменные, получаем

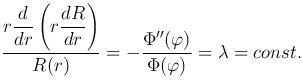
Следовательно, функция R(r) должна быть найдена из решения уравнения

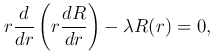
а для функции Φ(φ) получаем задачу на собственные значения

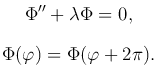
Здесь условие периодичности функции Φ(φ) является следствием периодичности искомого решения u(r, φ) по угловой переменной φ с периодом 2π.

Последняя задача имеет нетривиальные периодические решения только при λ=&lambda_n=n², n=0, 1, 2, … Эти решения имеют вид

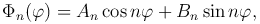
где A_n, B_n — произвольные постоянные.

Для функции R(r) при λ=n² получаем уравнение

()

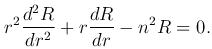Будем искать частные решения этого уравнения в виде степенной функции

тогда последнее уравнение примет вид

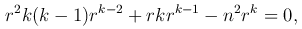
устанавливаем, что показатель k определяется из уравнения

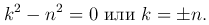
Следовательно, уравнение () имеет два линейно независимых решения: rⁿ и r^-n.

Решение внутренней задачи Дирихле должно быть ограничено в центре круга при r=0. Поэтому из двух найденных решений следует взять лишь

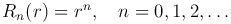
Таким образом, частные решения уравнения Лапласа в полярных координатах можно записать так:

В силу линейности и однородности равнения Лапласа суперпозиция частных решений

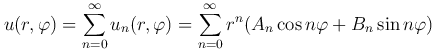
также будет удовлетворять этому уравнению.

Найдем постоянные A_n и B_n (n=0, 1, 2, …) .

Из граничного условия получим:

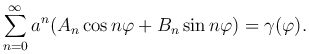
Разложим функцию γ(φ) в интервале (0, 2π) в тригонометрический ряд Фурье:

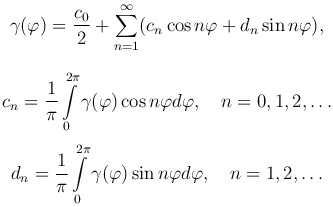
Приравняв коэффициенты в двух рядах, находим

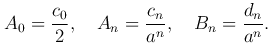
Тогда решение можно записать в форме

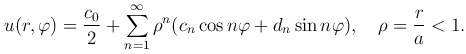
Замечание. Если в этой формуле считать ρ=a/r>1, то она будет определять решение внешней для круга задачи Дирихле.