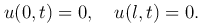Уравнение колебаний струны

Рассмотрим процесс колебаний тонкой упругой нити, которая может свободно изгибаться, не оказывая сопротивления изменению ее формы. В этом случае напряжения, возникающие в упругой нити, направлены по касательной к ее мгновенному профилю. Такую нить будем называть струной.

Пусть в положении равновесия струна расположена вдоль оси Ox. Будем рассматривать только поперечные колебания струны, считая, что перемещение частиц струны происходит в одной плоскости и все точки струны движутся перпендикулярно оси Ox. Обозначим через u(x, t) отклонение от положения равновесия точки струны с абсциссой x в момент времени t. При фиксированном значении t график функции u(x, t) представляет собой форму струны в момент времени t. А при фиксированном x функция u=u(x, t) определяет закон движения точки с абсциссой x. Эта точка движется по прямой, параллельной оси Ou. Скорость и ускорение точки:

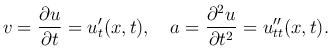
Рассматриваются только малые поперечные колебания струны, когда смещения u и производные ∂ u/∂ x столь малы, что их квадратами и произведениями можно пренебречь по сравнению со значениями самих величин. Тогда

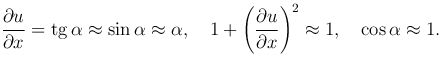
В этом случае длина дуги струны, ограниченной точками M₁(x₁, u₁) и M₂(x₂, u₂):

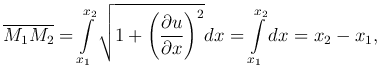
т.е. длина любого участка струны остается постоянной.

Обозначим через T натяжение струны. В случае малых натяжение в каждой точке струны не будет изменяться, то есть T=T₀=const. Силы натяжения в точках M₁ и M₂ направлены по касательной (обозначим через 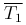и 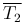). Спроектируем эти силы на ось Ou:

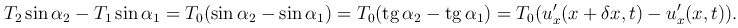
Применяя теорему Лагранжа о конечном приращении дифференцируемой функции, найдем

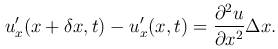
Через ρ(x) обозначим линейную плотность, которая характеризует распределение масс в струне. Масса участка струны будет равна m=ρ(x)δx.

Если на струну действуют также внешние силы, параллельные оси Ou, то величина равнодействующей этих сил, приложенных к участку 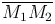приблизительно равна F(x, t)Δx, где F(x, t) — плотность распределения этих сил.

Тогда из второго закона Ньютона (ma=F) после сокращения на величину Δx получим, что процесс малых поперечных колебаний струны описывается дифференциальным уравнением второго порядка относительно искомой функции u(x, t):

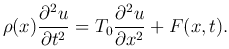
Это дифференциальное уравнение называется неоднородным одномерным волновым уравнением, или уравнением плоских волн. Это уравнение гиперболического типа. В случае постоянной линейной плотности ρ=ρ₀=const уравнение колебаний однородной струны принимает вид

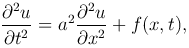
где 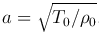, f(x, t)=F(x, t)/ρ₀.

Если f(x, t) ≡ 0, то однородное уравнение

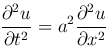
описывает свободные колебания струны без воздействия вынуждающей силы.

Замечание. Волновое уравнение описывает не только колебание струны, но и ряд физических процессов, которые называют волновыми. В частности, продолные колебания стержня постоянного поперечного сечения; плоские акустические волны в жидкостях и газах; распространение электрических возмущений в линии приотсутствии потерь; плоские электромагнитные волны в непроводящих средах.

Начальные и краевые условия

Чтобы из множества решений уравнения с частными производными второго порядка выбрать определенное решение, необходимо задать дополнительные условия.

Во-первых, нужно задать отклонение и скорость движения в начальный момент времени t₀ (обычно полагают t₀=0):

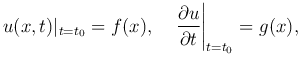
где f(x) и g(x) — заданные функции. Данные условия называются начальными условиями.

Во-вторых, зафиксировать отклонения концов струны. Если концы закреплены, то

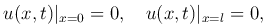
где l — длина струны. Эти условия называются краевыми или граничными условиями.

Таким образом, задача о колебаниях струны ставится следующим образом: Найти решение u=u(x, t) линейного уравнения с частными производными

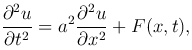
удовлетворяющее начальным условиям

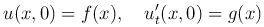
и краевым условиям