Уравнение колебаний струны

Рассмотрим свободные колебания бесконечной струны, то есть достаточно длинной струны, влиянием концов которой на процесс колебаний можно пренебречь.

Задача Коши для волнового уравнения:

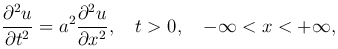(1)

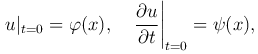(2)

где функции φ(x) и ψ(x) заданы на всей числовой оси.

Первое начальное условие определяет начальное отклонение струны от равновесного положения, а второе — начальный импульс, обусловливающий некоторое распределение скоростей частиц струны.

Решение этой задачи проведем методом Даламбера. Для этого введем новые независимые переменные

Преобразуя производные к новым переменным, найдем:

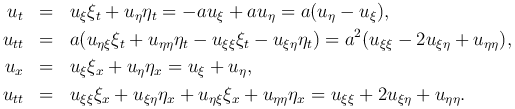
Уравнение (1) в новых переменных запишется в виде дифференциального уравнения для функции u(ξ, η):

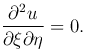
Этому уравнению удовлетворяет функция вида

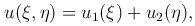
где u₁(ξ) и u₂(η) — произвольные дважды дифференцируемые функции. Следовательно, функция

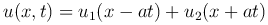
удовлетворяет уравнению (1).

Функции u₁, u₂ определяются таким образом, чтобы удовлетворялись начальные условия (2). Тогда

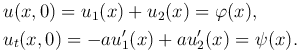
Интегрируя второе равенство в пределах от x₀ до x, получаем

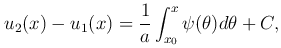
где x₀ и C — постоянные.

Решая систему уравнений, получим

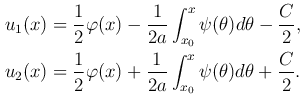
Отсюда найдем, что

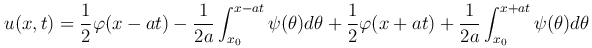
или

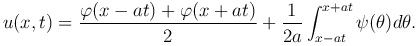
Если функция φ(x) имеет производные до второго порядка включительно, а функция ψ(x) — до первого порядка, то эта формула определяет решение задачи Коши (1), (2). При этом данная формула называется формулой Даламбера.