Задача о колебаниях ограниченной струны

Задача о колебаниях ограниченной струны: найти решение u=u(x, t) уравнения

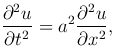(1)

которое удовлетворяет начальным условиям:

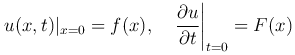
(f(x) и F(x) — заданные функции определенные на отрезке [0, l]) и краевым условиям:

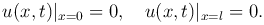
Для решения поставленной задачи применяется метод Фурье. Решение u(x, t) будем искать в виде

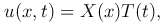
где X(x) — функция только от x; T(t) — функция только от t. Подставим в уравнение для частных производных (1), получим:

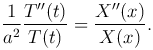
Левая часть не зависит от x, а только от t. Правая часть не зависит от t, а только от x. Но поскольку функция u(x, t) =X(x) T(t) — решение уравнения (1), то последнее равенство должно выполняться для всех x и всех t. Это возможно лишь тогда, когда обе части не зависят ни от x, ни от t, т.е. являются постоянными. Следовательно

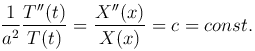
В результате получим два обыкновенных дифференциальных уравнения второго порядка с постоянными коэффициентами:

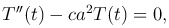(2)

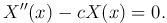(3)

Начальные условия дают:

т.к. ищем нетривиальное решение (u(x, t)≠0), то

Характеристическое уравнение для (3):

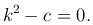
Возможны три случая:

1. Если c>0, c=λ². Тогда корни характеристического уравнения k_1,2=±&lambda. Общее решение:

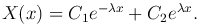
Из краевых условий:

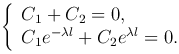
Определитель системы: 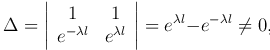, то система имеет единственное решение C₁=C₂=0. То есть получаем тривиальное решение X(x)≡0.

2. Если c=0, то k_1,2=0. тогда получим решение X(x)=C₁+C₂x. Краевым условиям удовлетворяет только X(x)≡0.

3. Если c=-λ<0, то k_1,2=±λ i и решение:

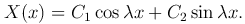
Из краевых условий получим

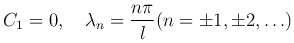
Таким образом, каждая из функций

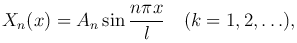
где A_n — произвольная постоянная, являются решениями.

Постоянные λ_n называются собственными числами, а функции

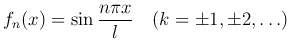
— собственными функциями уравнения (3).

В уравнении (2): т.к. c=-λ², 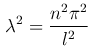, то получим

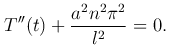
Характеристическое уравнение

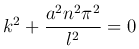
имеет мнимые корни 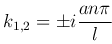, следовательно, общее решение уравнения (2):

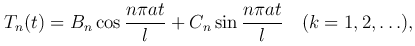
где B_n, C_n — произвольные постоянные.

Таким образом,

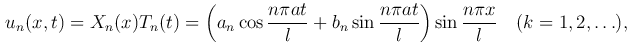
где a_n=A_nB_n, b_n=A_nC_n.

Каждая из этих функций является решением уравнения (1), удовлетворяющая краевым условиям, и называется собственной функцией этого уравнения, а колебания, определяемые ею, называются собственными колебаниями.

Составим ряд

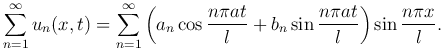
Эта функция также является решением уравнения (1), причем это решение удовлетворяет краевым условиям. Коэффициенты ряда a_n и b_n выберем так, чтобы они удовлетворяли начальным условиям:

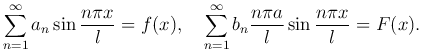
Следовательно, f(x) и F(x) представляют собой разложение в ряд Фурье по синусам в промежутке [0, l]. Коэффициенты разложения определяются по формулам:

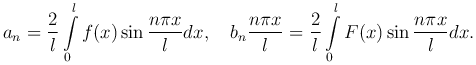
Таким образом,