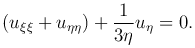Уравнения математической физики
Каноническая форма уравнения Трикоми
Пример. Привести уравнение Трикоми к каноническому виду.
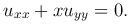
При x < 0 это уравнение гиперболического типа. Его характеристическое уравнение принимает вид
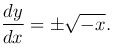
Поэтому кривые
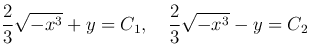
являются характеристиками уравнения Трикоми. С помощью преобразования
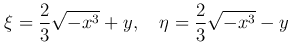
выразим производные через новые переменные:
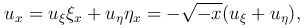
так как
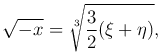
то
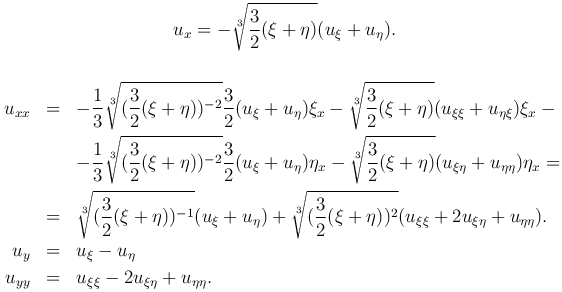
Тогда уравнение Трикоми преобразуется к каноническому виду
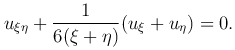
Если x > 0, то имеем уравнение эллиптического типа. Его характеристическое уравнение принимает вид
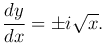
Интегральные кривые этого уравнения
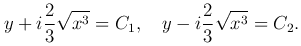
Преобразованием
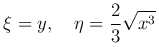
приводим уравнение Трикоми к каноническому виду:
