 Механика
Механика
 Ускорение материальной точки
Ускорение материальной точки
По аналогии со скоростью, можно ввести быстроту изменения скорости — ускорение. При перемещении точки за время Δt, радиус-вектор изменится на Δr, а скорость изменится на Δv. Средним ускорением называется вектор aср равный отношению вектора изменения скорости Δv к промежутку времени Δt:
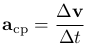
Направление вектора aср совпадает с направлением вектора изменения скорости Δv.
Мгновенным ускорение или просто ускорением точки в момент времени t называется предел среднего ускорения при Δt→0:
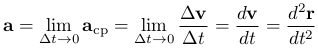
Ускорение точки равно первой производной от ее скорости v по времени Δt или второй производной радиус-вектора r по времени Δt.
Вектор ускорения можно спроектировать на координатные оси:
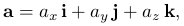
где компоненты ускорения равны
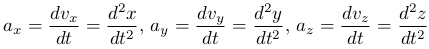
Модуль ускорения вычисляется по формуле:
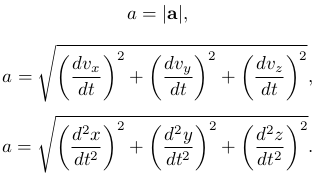
Рассмотрим движение тела по траектории из точки M в точку N за время от t до t+Δt (рисунок 1). Обозначим длину вектора v1 через v (отрезок MB). Перенесем начало вектора v2 из точки N в точку M (соответствующий отрезок MD имеет длину v+Δv). Тогда приращение скорости за время Δt будет Δv=v2-v1 (соответствующий отрезок BC).
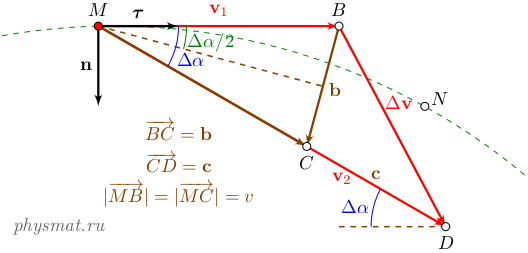
Рис. 1 Вычисление ускорения точки
Введем локальную систему координат с началом отсчета в точке M и взаимно перпендикулярными ортами (единичными радиус-векторами) τ (направлен по касательной к траектории в точке M, вдоль вектора v1) и n (направлен в направлении вогнутости траектории, называется единичным вектором главной нормали). Разложим вектор приращения скорости Δv в новой системе координат.
Отложим на стороне MD отрезок MC длиной v. Введем два вектора: вектор b с началом в точке B и концом в точке C и вектор c в начале точки C и концом в точке D. Разложим в новой системе координат вектор приращения скорости Δv
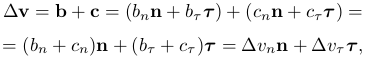
где индексы n и τ — проекции на координатные оси, определяемые ортами n и τ, соответственно.
Найдем компоненты векторов b и c.
Треугольник BMC равносторонний с двумя сторонами равными v и углом между ними Δα, следовательно, длина вектора b и его компоненты равны:
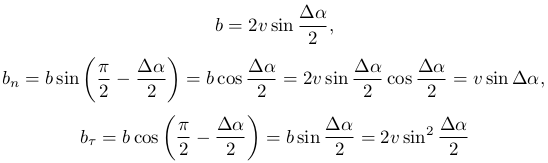
Длина вектора c определяется как разность длины вектора v2 и вектора v. Угол между вектором c и осью τ равен Δα. Получим:
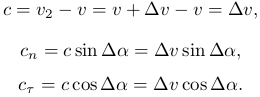
Скорость v1 в точке M фиксирована и равна v, орты n и τ также фиксированы в этой точке. Если устремить Δt→0, то
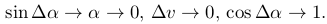
Найдем ускорение a в точке M используя разложение приращения скорости в новой системе координат:
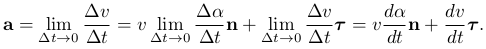
Таким образом, разложение ускорения в новой системе координат записывается в виде:
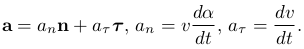
Смысл компонент ускорения следующий: an определяет быстроту изменения направления скорости и называется нормальным ускорением, а aτ определяет быстроту изменения величины ускорения и называется тангенциальным (или касательным) ускорением.
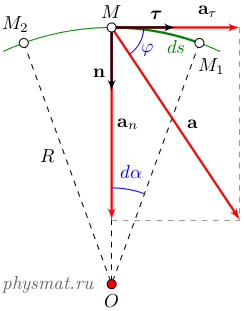
Рис. 2 Компоненты ускорения при криволинейном движении
Рассмотрим малое перемещение материальной точки по траектории из точки M в точку M1 (рисунок 2). Пройденный путь равен длине дуги MM1 и составляет ds. Выберем три близкие друг к другу идущие подряд по траектории движения точки M2, M и M1. При сближении точек M2→M и M1→M проведем через них окружность. Окружность называется соприкасающейся, а ее радиус R и центр O называются радиусом кривизны и центром кривизны траектории в точке M. Главная нормаль n и нормальное ускорение an в точке M направлено в сторону центра кривизны O. Тангенциальное ускорение направлено по касательной к окружности.
Длина дуги ds может быть вычислена по значениям радиуса окружности R и углу опирающемся на эту дугу: ds = R dα. Выразим из этого соотношения угол α и подставим его в выражение для нормальной компоненты ускорения:
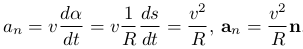
Проекция нормального ускорения всегда положительна, следовательно, вектор нормального ускорения всегда направлен по главной нормали к центру кривизны траектории. Чтобы подчеркнуть это нормальное ускорение также называют центростремительным ускорением.
Величина полного ускорения равен
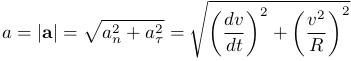
Направление ускорение a определяется углом φ между векторами a и τ:
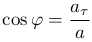
В стандартной системе единиц СИ размерность ускорения метр в секунду в квадрате (м/с²).
Использованная литература: