 Механика
Механика
 Сила
Сила
Состояние механического движения тела может измениться в результате действия на него других тел. Степень механического действия тел друг на друга определяется понятием силы. Сила, действующая на тело (или приложенная к телу) есть физическая величина, являющаяся мерой механического действия на это тело со стороны другого тела. Движение, в результате воздействия других тел, можно описать как движение тела под действием приложенных к нему сил.
Для определения силы, приложенной к телу, необходимо знать величину силы, ее направление и точку приложения. Прямая, проведенная через точку приложения силы в направлении действия этой силы, называется линией действия силы.
Для определения численного значения силы, необходимо сравнить ее с эталоном силы, то есть с силой, принимаемой в данной системе единиц за единицу.
Рассмотрим способ измерения силы. Возьмем пружинный динамометр и подвесим груз известной величины. При этом, пружина растянется на величину x1 действием силы F1. Из опыта известно, что растяжение пружины пропорционально действующей на нее силы:
F = k x, ( )
)
где k — коэффициент пропорциональности, называемый коэффициентом упругости пружины.
Если разместить другой груз (с отличной массой), то пружина растянется на величину x2 действием силы F2. При одновременном размещении обоих грузов пружина растянется на величину x3=x1+x2 действием силы F3=F1+F2. Подставляя измеренные значения можно провести проверку зависимости ( ). Опытным путем установлено, что малых растяжениях пружины эти зависимости выполняются с высокой точностью, что позволяет проградуировать динамометр для измерения силы неизвестной величины.
). Опытным путем установлено, что малых растяжениях пружины эти зависимости выполняются с высокой точностью, что позволяет проградуировать динамометр для измерения силы неизвестной величины.
Если к одной точке одновременно приложить две силы равные по величине и противоположно направленные, то их действие не вызывает механического движения, поскольку силы взаимно уравновешиваются.
Уравновешивая силу с помощью пружинного динамометра можно определить ее величину и направление. Если пружина растягивается, то сила направлена вдоль оси пружины от динамометра, если сжимается, то сила направлена от тела к динамометру.
Опытным путем установлено, что если к точке тела приложить две силы, то их можно уравновесить одной силой приложенной к той же точке. Величина этой силы численно равна, а направление противоположно геометрической сумме двух приложенных сил. То есть сила является векторной величиной.
Если на точку тела действует несколько сил, то их можно заменить одной эквивалентной силой равной геометрической сумме всех приложенных к точке тела сил:
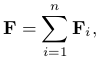
приложенную к той же точке. Эту силу F называют результирующей (или равнодействующей) силой. Для того, чтобы приложенные к точке тела силы уравновешивали друг друга необходимо, чтобы равнодействующая сила была равна нулю.
Действие силы на абсолютно твердое тело не меняется при переносе точки приложения в любую другую точку, лежащую на линии действия силы.
Тело называют свободным, оно не ограничено другими телами в пространстве и может совершать произвольные движения. Часто тело ограничено в пространстве или может совершать только некоторые движения. Например, шарик подвешенный на нерастяжимой ники не может переместиться дальше длины нити относительно точки подвеса; вал электродвигателя может совершать только вращательные движения, а поршень двигателя, только поступательные. Любые ограничения на возможное положение тела в пространстве или ограничение движения называют связами, наложенными на это тело.
При изучении движения несвободных тел используют принцип освобождаемости: несвободное тело или система тел может рассматриваться как свободная, если заменить все наложенные на него связи и действия тел осуществляющие связи на соответствующие силы. Эти силы называются реакциями связей, а все остальные силы, действующие на тело — активными силами.
Обычно, при решении динамических задач, активные силы известны, а реакции связи нужно определить в ходе решения задачи. При решении задачи с активными и реакциями связей движение тела должны соответствовать его движению при учете ограничивающих связей. Рассмотрим пример скатывания шарика по наклонной плоскости. Активной силой будет сила тяжести, а реакцией связи будет сила реакции плоскости, обычно раскладываемая на две составляющие: перпендикулярная к плоскости нормальная реакция и касательная (тангенциальная) составляющая, характеризующая силу трения. Сила тяжести есть заданная величина, поэтому нормальная реакция выбирается такими образом, чтобы шарик двигался вдоль плоскости и расстояние от центра шарика до плоскости всегда оставалось равным радиусу шарика.
Поскольку ограничения движения тела связаны с соответствующими силами, реакциями связей, то при изучении движения тела под действием сил всегда используют принцип освобождаемости рассматривая движение свободного тела под действием всех активных сил и всех реакций связей.
Использованная литература