 Механика
Механика
 Кинетическая и потенциальная энергия
Кинетическая и потенциальная энергия
Мера механического движения, определяемая работой, которую необходимо совершить для полной остановки движения тела, называется кинетической энергией Wc. Рассмотрим твердое тело B массой m, движущееся со скоростью v. Пусть тело B сталкиваясь с твердым телом C полностью останавливается. Во время взаимодействия тело B действует на тело C с силой F и на молом участке ds совершает работу
δA = Fτ ds
По третьему закону Ньютона со стороны тела C на тело B действует сила -F с касательной составляющей -Fτ замедляющей движение тела B. По второму закону Ньютона
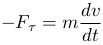
Подставляя это выражение в соотношение для элементарной работы
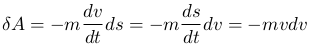
Работа, совершаемая телом B до полной остановки,
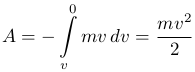
Кинетическая энергия Wc=A:
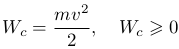
Кинетическая энергия тела не может быть отрицательной, зависит от инертности тела (массы) и кинематических характеристик (скорости) и не зависит от причин, из-за которых тело приобрело эту скорость (силы). Значение кинетической энергии зависит от выбранной системы отсчета, следовательно данная величина является относительной, а не абсолютной.
Если различные части тела движутся с разной скоростью или рассматривается произвольная система движущихся с различной скоростью тел, то кинетическая энергия тела или системы тел находится как сумма кинетических энергий материальных точек составляющих тело или тел составляющих систему (для n точек/тел с массами mi и скоростями vi):
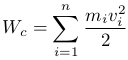
Если на систему тел действуют потенциальные силы, то можно ввести физическую величину, характеризующую работу, которую необходимо совершить для измерения пространственного положения тел в системе. Конфигурация системы определяетсяпотенциальной энергией Wp, а работа A12 совершаемая для изменения этой конфигурации — изменение потенциальной энергии:
A12 = Wp1 - Wp2.
Изменение потенциально энергии не зависит от траектории перемещения тел, поскольку работа, совершаемая консервативными силами, не зависит от траектории перемещения, следовательно, потенциальная энергия является функцией координат. В случае незамкнутой системы, предполагается, что внешние консервативные силы стационарны, то есть могут меняться только вследствие изменения положения тел, входящих в систему.
При элементарном изменении конфигурации системы работа является полным дифференциалом и равна убыли потенциальной энергии системы:
dA = -dWp.
Экспериментально измерить можно только работу, а поскольку работа идет на изменение потенциальной энергии, то потенциальную энергию можно определить только с точностью до константы или, так называемой, потенциальной энергии нулевой конфигурации системы.
Сила тяжести вблизи поверхности Земли является потенциальной силой. Рассмотрим перемещение тела массой m с высоты H на поверхность Земли. Затрачиваемая на это перемещение работа равна A=mgH. При перемещении по склону длиной l и составляющей угол α работа будет составлять A=mgl cos α=mgH. Если тело движется по криволинейной траектории, то разбив ее на прямолинейные участи и просуммировав получим также значение A=mgH. То есть работа по перемещению тела в поле тяжести зависит только от высоты начального и конечного положения тела. При движении по замкнутой траектории в начальную точку совершаемая работа будет равна нулю, что доказывает консервативность силы тяжести. Изменение потенциальной энергии равно
Wp - Wp0 = A = mgH
Принимая потенциальную энергию на поверхности Земли равную нулю Wp0=0, получим
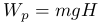
Найдем потенциальную энергию сжатой пружины. Сила упругости сжатой на величину x пружины равна
F = - kx.
Элементарная работа на сжатие пружины на величину dx равно
dA = F dx = - kx · dx.
Работа силы упругости при конечном изменении сжатия тела на величину x из свободного состояния x=0 равна
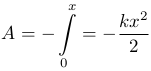
Если принять потенциальную энергию недеформированной пружины равной нулю, то потенциальная энергия сжатой пружины будет равна
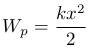
В зависимости от вида консервативных сил, действующих на систему, можно рассматривать внутреннюю и внешнюю потенциальную энергию. Полная потенциальная энергия равна сумме внутренней и внешней потенциальных энергий:
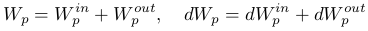
В рассмотренных выше примерах, потенциальная энергия тела в поле тяжести является внешней (так как обусловлена внешней силой тяжести), а потенциальная энергия сжатой пружины является внутренней (так как обусловлена внутренними силами возникающими в пружине).
Полная механическая энергия системы равна сумме кинетической и потенциальной энергий:
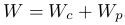
Полная механическая энергия системы тел (или системы материальных точек) зависит только от масс, скоростей и координат всех составляющих систему частей.
Использованная литература