Механика
Простейшие виды движения материальной точки
Равномерное прямолинейное движение вдоль оси Ox. Начальную координату точки в момент времени t=0 обозначим через x0. При этом виде движения скорость vx (при наличии только одной компоненты скорости v=vx) не меняется ни по величине, ни по направлению, следовательно
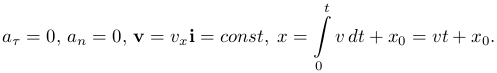
Величина скорости vx положительна при движении точки в положительном направлении оси и отрицательна при движении в противоположном направлении. Длина пути пройденного точной за промежуток времени от 0 до t:
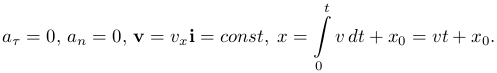
Равнопеременное прямолинейное движение вдоль оси Ox. Начальную координату точки в момент времени t=0 обозначим через x0, а начальную скорость через v0. Направление движения не меняется, значит an=0. Величина скорости меняется на одинаковую величину за равные промежутки времени, то есть тангенциальное ускорение постоянно aτ=const. Если направления вектора ускорения и вектора скорости совпадают, то скорость со временем возрастает и движение будет равноускоренным, если вектора направлены в противоположные стороны, то скорость со временем уменьшается и движение будет равнозамедленным. Найдем величину скорости v
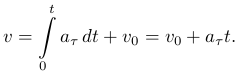
При равнозамедленном движении v и aτ имеют разные знаки (вектора скорости и ускорения направлены в противоположных направлениях) и можно вычислить время, за которое точка остановится (то есть текущая скорость станет равной нулю v=0):
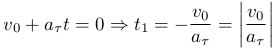
После промежутка времени t1 движение станет равноускоренным (направления векторов v и aτ совпадают)
Координата вычисляется следующим образом:
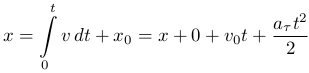
Пройденный путь будет равен
(
)
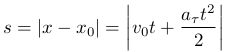При равнозамедленном движении мы можем вычислить максимальный путь пройденный в одном направлении. По определению экстремума возьмем производную от последнего выражения и получим v0 + aτt=0, что соответствует рассмотренному ранее случаю остановки точки. Подставим полученное значение времени t1 в выражение для пройденного пути и получим
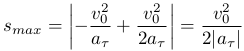
Также, при равнозамедленном движении можно вычислить время необходимое для того, чтобы точка вернулась в первоначальное положение x0, то есть пройденный путь будет равен нулю. Подставляя s=0 в выражение (), получим (исключая тривиальный случай при t=0 когда точка уже находится в первоначальном положении):
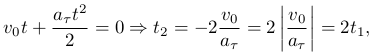
то есть точка возвращается в первоначальную координату (пройдя расстояние 2 smax) за удвоенное время перемещения на smax, что полностью согласуется с определением равнопеременного движения.
Запишем уравнения равноускоренного движения для скорости и пройденного пути:
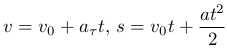
Эти уравнения можно рассматривать как систему двух параметрически заданных уравнений с параметром t. Если выразить t из первого уравнения t=(v-v0)/aτ и подставить его во второе уравнение, то можно исключить время и связать три величины: путь, скорость и ускорение:
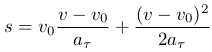
Если в начальный момент времени t=0 скорость равна нулю (v0=0), то последнее выражение упростится. Любую величину можно выразить через две другие:
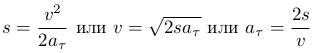
Рассмотрим пример равнопеременного движения. Если направить ось Ox вертикально вверх, то брошенное с уровня земли со скоростью v0 (v0 положительно, поскольку направление совпадает с положительным направлением оси Ox) вверх тело будет двигаться равнозамедлено с ускорением aτ=-g, где g ускорение свободного падения (aτ отрицательно, поскольку ускорение свободного падения направлено к земле в отрицательном направлении оси Ox). Тело поднимется на максимальную высоту H за время t1, после чего упадет на землю за время t2 от момента броска. По полученным ранее формулам можно вычислить эти величины:
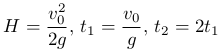
Отметим, что значение ускорения свободного падения одинаково для всех тел и зависит только от высоты над уровнем моря и географической широты места проведения опыта. В вычислениях, не требующих высокой точности можно брать значение g=9,81 м/с².
Движение вверх до максимальной высоты H будет равнозамедленным, а падение вниз — равноускоренным.
Равномерное движение по окружности радиусом R является примером простейшего криволинейного движения. Вектор скорости меняет свое направление an≠0, но не меняет своей величины (aτ=0). Ускорение материальной точки совпадает с вектором нормального ускорения имеющего величину
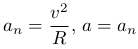
За время t=T точка полностью пройдет по окружности и вернется в начальную точку. Величину T называют периодом движения по окружности. Поскольку длина окружности равна l=2πR, то
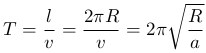
Величина, обратная периоду, называется линейной частотой f:
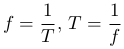
Линейная частота имеет размерность обратной секунды (1/с) и означает количество оборотов, совершаемых точкой, при движении по окружности.
Круговая или циклическая частота ω равняется углу, измеряемому в радианах, описываемому радиусом-вектором точки на окружности в единицу времени (размерность радиан в секунду, рад/с). Поскольку за полный оборот радиус-вектор описывает угол равный 2π радиан, то угловая частота равна
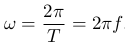
Скорость равномерного движения по окружности равна:
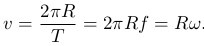
Ускорение равномерного движения по окружности:
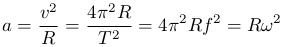
Отметим, что приведенные формулы относятся к криволинейному равномерному движению материальной точки по окружности (например, движению спутника по круговой орбите вокруг Земли). Поскольку материальная точка не имеет размеров, то не следует путать такое движение с вращением (например, вращением диска). В следующем разделе будет рассмотрено вращательное движение абсолютно твердого тела с выводом уравнений для вращательного движения.
Использованная литература: