Геометрическая оптика

Длины воспринимаемых глазом световых волн очень малы (порядка 10^-7 м). Поэтому распространение видимого света можно в первом приближении рассматривать, отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В предельном случае, соответствующем λ → 0, законы оптики можно сформулировать на языке геометрии. В соответствии с этим раздел оптики, в котором пренебрегают конечностью длин волн, называется геометрической оптикой. Другое название — лучевая оптика.

Основу геометрической оптики образуют четыре закона:

1. закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно. Этот закон является приближенным: при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.
2. закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.
3. закон отражения света утверждает, что отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; угол отражения θ₁ равен углу падения θ: θ=θ₁.
4. закон преломления света утверждает, что преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной в точке падения; отношение синуса угла падения θ к синусу угла преломления θ₂ есть величина постоянная для данных веществ.

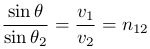
n₁₂ = n₂/n₁ — относительный показатель преломления. θ_l = arcsin n₁₂ является предельным углом, при котором происходит явление полного внутреннего отражения.

В основу геометрической оптики может быть положен принцип, установленный Ферма в середине XVII столетия. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света.

В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

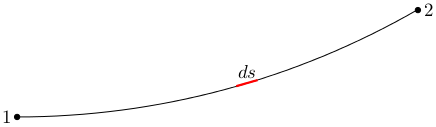
Оптический путь
Рис. 1

Участок пути ds (рис. 1) свет проходит за время dt = ds/v, где v — скорость света в данном месте. Так как v = с/n, то dt = nds/c, и время τ для прохождения светом пути 1 → 2 равно

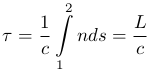
где L называют оптической длиной пути. В однородной среде L = ns.

Уравнение тонкой линзы. Фокус

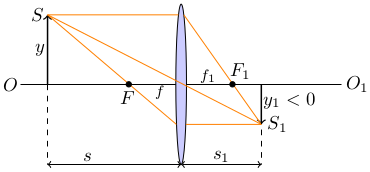
Тонкая линза
Рис. 2

Простейшей центрированной оптической системой является линза. Она представляет собой прозрачное (обычно стеклянное) тело, ограниченное двумя сферическими поверхностями (в частном случае одна из поверхностей может быть плоской). Точки пересечения поверхностей с оптической осью линзы называются вершинами преломляющих поверхностей. Расстояние между вершинами именуется толщиной линзы. Если толщиной линзы можно пренебречь по сравнению с меньшим из радиусов кривизны ограничивающих линзу поверхностей, линза называется тонкой. Формула тонкой линзы в воздухе:

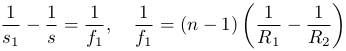
где s и s₁ — расстояния от линзы до источника S и его изображения S₁, f — заднее фокусное расстояние (от линзы до заднего фокуса F₁). Здесь принято следующее правило знаков: отрезки, отсчитываемые от линзы против хода лучей, т. е. влево на рис. 2, считаются отрицательными, а по ходу лучей (вправо от линзы) — положительными. На рисунке показан случай, когда s₁>0, a s<0. Это относится и к радиусам кривизны поверхностей линзы, R₁ и R₂ — передней и задней. Для линзы, изображенной на рисунке, R₁>0, а R₂<0.

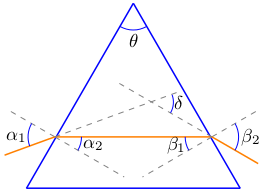
Преломление света в призме

Преломление света в призме
Рис. 3

Треугольная призма представляет собой тело с двумя треугольными основаниями, соединенными тремя прямоугольными гранями. Рассмотри прохождение света через призму в плоскости параллельной основаниям. На рисунке показано сечение призмы этой плоскостью и траекторию прохождения луча. Если угол при вершине призмы θ, а угол падения входящего луча α₁ (измеряется относительно перпендикуляра к плоскости падения), то угол преломления входящего луча α₂, а также углы падения β₁ и преломления β₂ исходящего луча определяются из соотношений для преломления света (для малых углов θ и α₁):

α₁ ≈ sin α₁ = n sin α₂ ≈ n α₂,
β₂ ≈ sin β₂ = n sin β₁ ≈ n β₁.

Рассмотри четырехугольник образованный входящим и исходящим лучами и их перпендикулярами к поверхности. Поскольку сумма углов четырехугольника равна 2π, получим

π - δ + π - θ +α₁ + β₂ = 2π

Подставляя соотношения для преломления света и учитывая, что сумма углов треугольника равна π (для треугольника образованного перпендикулярами входящего и исходящего лучен и луча внутри призмы) найдем угол отклонения луча при прохождении через призму δ:

δ = α₁ + β₂ - θ = n·(α₂+β₁) - θ = n θ - θ = (n-1)·θ.

Таким образом, при преломлении в призме с малым преломляющим углом θ луч отклоняется от своего первоначального направления на угол δ =(n-1)·θ независимо от угла падения, если он также мал.