Оптика
Определение главных фокусных расстояний линз
Приборы и принадлежности: оптическая скамья, осветитель с матовым или молочным стеклом, ползушка с линзой, экран, собирающая и рассеивающая линзы, линейка с миллиметровыми делениями.
Цель работы: определение фокусного расстояния собирающей линзы.
Ввиду малости световых волн (диапазон видимого спектра 400-700 нм), оказывается возможным выделить из широкого потока света сравнительно узкую ее часть без существенного нарушения прямолинейности распространения, вследствие дифракции. Такой прямолинейно распространяющийся узкий пучок света называется световым лучом. Световыми лучами можно управлять с помощью линз, зеркал, призм и т.д.
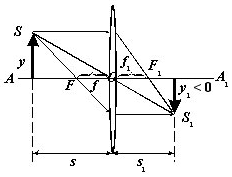
Рис. 1
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Линия, проходящая через центры этих поверхностей, называется главной оптической осью. В дальнейшем мы будем иметь в виду лучи, проходящие вблизи главной оптической оси (параксиальные лучи). Все лучи, параллельные главной оптической оси, пересекаются в одной и той же точке оси F - главном фокусе. Точка линзы (точка O на рис. 1), проходя через которую лучи не изменяют своего направления, называется оптическим центром линзы. Расстояние между главным фокусом и оптическим центром называется главным фокусным расстоянием.
В формулах, связывающих геометрические параметры оптической системы, принято правило знаков, согласно которому линейные размер считается отрицательным, если отрезок, его выражающий, располагается по ту сторону линзы, откуда распространяется свет и положительным, если отрезок лежит в стороне, куда распространяется свет. В первом случае значение величины входит в формулу со знаком минус (например: s = -|s| на рис. 1), во втором - со знаком плюс (s1 = |s1|). Таким образом, все отрезки в оптической системе являются алгебраическими величинами.
На рис. 1 показаны основные точки оптической системы и даны основные определения: AA1 - главная оптическая ось; F и F1 - передний и задний фокусы оптической системы; f и f1 - переднее и заднее фокусные расстояния; s и s1 - расстояния от линзы до предмета и до изображения; y и y1 - поперечные размеры предмета и изображения.
Величину Φ=1/f1 называют оптической силой линзы, которую измеряют в диоптриях (дптр): 1 дтпр = 1 м-1. Величину β = y1/y называют линейным или поперечным увеличением линзы. Можно показать, что β = s1/s.
Фокусное расстояние можно вычислить по формуле:
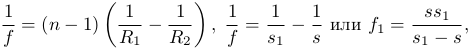(1
)
где f1 - заднее фокусное расстояние, n - показатель преломления вещества линзы; R1 и R2 - радиусы сферических поверхностей линзы.
Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. В точках этой плоскости (побочных фокусах), пересекаются пучки параллельных лучей, идущих под некоторым углом к главной оптической оси.
Определение знака фокусного расстояния подчиняется правилу знаков. При построение изображений, получаемых с помощью собирающих линз, пользуются фокусами от линзы со стороны, противоположной предмету. Поэтому фокусное расстояние собирающей линзы имеет положительное значение. При построении мнимых изображений, получаемых с помощью рассеивающих линз, используется фокус, лежащий от линзы по туже сторону, что и предмет. Поэтому фокусное расстояние рассеивающей линзы имеет отрицательное значение.
Горизонтальная оптическая скамья составлена из двух параллельных металлических стержней, свободно входящих своими концами в трубки, благодаря чему скамья может быть раздвинута на необходимую длину. Так как стержни и трубки имеют различную толщину, то прибор снабжен ползунками двойного рода: одни предназначены для стержней, другие для трубок.
На одном из концов скамьи установлен экран с круглым осветителем, на котором изображена стрелка, служащая предметом. Отверстие со стрелкой освещается фонарем, снабженным матовым стеклом.
Изображение A1B1(A2B2) предмета AB, полученное с помощью линзы, рассматривается на экране, помещенном на противоположном конце скамьи. Линзы устанавливаются на такой высоте, при которой перекресток оказывается лежащим на уровне главной оптической оси линзы. Плоскость экрана должна быть перпендикулярна этой оси. Расстояние между приборами измеряется при помощи линейки с миллиметровыми делениями, прикрепленной к скамье.
Главное фокусное расстояние линзы можно определить непосредственно, измеряя расстояние от линзы до предмета и до изображения, воспользовавшись затем уравнением (1).
Однако величины s и s1 измерить точно нельзя, в силу того, что в общем случае оптический центр линзы не совпадает с центром симметрии и найти его положение трудно.
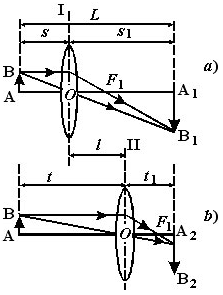
Рис. 2
Поэтому мы будем пользоваться более совершенным методом, называемым методом Бесселя. Сущность этого метода заключается в следующем. Если расстояние L от предмета до экрана больше 4f, то всегда можно найти два таких положения линзы (рис. 2), при котором на экране получается отчетливые изображения предмета: в одном случае - рис. 2a) - увеличенное, в другом - рис. 2b) - уменьшенное.
В первом положении линзы можно выразить фокусное расстояние, пользуясь формулой (1), соблюдая при этом правило знаков (обозначения указаны на рис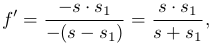.2):
(2)
Аналогично для второго положения:
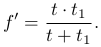(3)
Каждая из сумм в знаменателе правой части равенства (2) и (3) равна расстоянию L между предметом и экраном, поэтому:
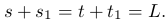(4)
В таком случае должны быть равны и числители правой части равенств (2) и (3)
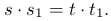(5)
Однако совместное существование равенств (4) и (5) возможно лишь при условии, если s=t, s1=t1 или s=t1, t=s1. Первое невозможно по условию опыта. Следовательно, остается в силе лишь второе условие.
Обозначим расстояние между оптическими центрами линзы в I и II положениях через l. Тогда из рис. 2 видно, что
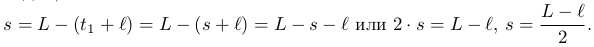
Расстояние
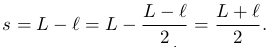
Воспользовавшись формулой (2), выразим фокусное расстояние линзы:
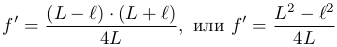(6)
Задача, таким образом, сводится к измерению перемещения любой точки линзы или даже подставки, на которой линза закреплена.
) вычислить главное фокусное расстояние линзы.
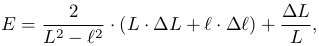
где Δ L - равно двум половинкам наименьшего деления шкалы, 1 мм.
| N опыта | l, см | Δl, см | L, см | ΔL, см |
|---|---|---|---|---|
| Среднее |
Приборы и принадлежности: оптическая скамья, осветитель с матовым стеклом, ползушка с рассеивающей линзой, линейка с миллиметровыми делениями.
Цель работы: определение фокусного расстояния рассеивающей линзы.
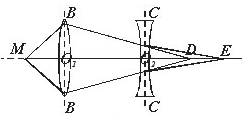
Рис. 3
Если на пути лучей, выходящих из точки М и сходящихся после преломления в линзе BB в точке D (рис. 3), поставить рассевающую линзу СС так, чтобы её расстояние от точки D было меньше её фокусного расстояния, то изображение точки М удалиться от линзы ВВ, переместившись в точку Е.
Основываясь на принципе обратимости световых лучей в системах линз, мы можем рассматривать лучи, изображенные на рис. 3, как выходящие из точки Е и собирающиеся в точке М. Тогда точка D будет мнимым изображением точки Е после преломления лучей в рассевающей линзе СС.
Обозначая расстояния точек Е и D от линзы до СС соответственно через s и s' можно, пользуясь формулой (1), вычислить фокусное расстояние рассеивающей линзы, учитывая при этом, что, согласно правилу знаков, числовые значения s и s' войдут в формулу (1) со знаком минус.
).
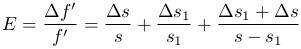
имея в виду, что δ S = δ L2 + δ L0 и δ S1 = δ L1 + δ L0.
| N опыта | L0, см | ΔL0, см | L1, см | ΔL1, см | L2, см | ΔL2, см |
|---|---|---|---|---|---|---|
| Среднее |