Волны

Волнами называются возмущения, распространяющиеся в среде (или в вакууме) и несущие с собой энергию. Характерное свойство волн состоит в том, что перенос энергии волной осуществляется без переноса вещества. Основными видами волн являются упругие волны (в частности, звуковые и сейсмические), волны на поверхности жидкости и электромагнитные волны (световые волны, радиоволны и др.). Несмотря на большое разнообразие физических процессов, вызывающих волны, их образование происходит по общему принципу. Возмущение, происшедшее в какой-нибудь точке А среды в некоторый момент времени, проявляется спустя определенное время на интересующем нас расстоянии от точки А, т.е. передается с определенной скоростью.

Волны могут иметь различную форму. Одиночной волной или импульсом называется короткое возмущение, не имеющее регулярного характера (рис. 1. а). Ограниченный ряд повторяющихся возмущений называется цугом волн. Обычно под цугом понимают отрезок синусоиды (рис. 1. б). Особое значение в теории волн имеет гармоническая волна, т. е. бесконечная синусоидальная волна, в которой изменение состояния среды происходит по закону синуса или косинуса (рис. 1 в).

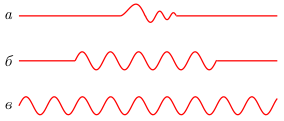
Рис. 1

При волновом процессе частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны (или волновым фронтом). Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными. Волновой фронт все время перемещается. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне — множество концентрических сфер.

Уравнение волны

Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат х, у, z и времени t:

Ψ = Ψ (x, y, z; t). (1)

Рассмотрим гармонические колебания, тогда (1) можно записать как

Ψ = a cos (ω t + α),

здесь ω t + α называется фазой волны, a — амплитудой волны, ω — циклической (круговой) частотой колебаний частиц среды (размерность с^-1), α — начальная фаза.

Периодом колебаний называют величину

T = 2π / ω.

Найдем уравнение для плоской волны. Если v — скорость распространения волны, то время необходимое волне пройти путь от x = 0, до x будет τ = x/v. Следовательно колебания при x = 0 и x будут отставать друг от друга на время τ и

Ψ(x, t) = a cos [ω(t-τ)+α] = a cos [ω(t-x/v)+α], (2)

Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси x, выглядит следующим образом:

Ψ = a cos [ω(t-x/v)+α]. (3)

Величина a представляет собой амплитуду волны. Начальная фаза волны α определяется выбором начал отсчета х и t. При рассмотрении одной волны начала отсчета времени и координаты обычно выбираются так, чтобы α была равной нулю. При совместном рассмотрении нескольких волн сделать так, чтобы для всех них начальные фазы равнялись нулю, как правило, не удается.

Зафиксируем какое-либо значение фазы, стоящей в уравнении (3), положив

Ψ = a cos [ω(t-x/v)+α].

Тогда dx/dt=v_p будет скоростью распространения этого (зафиксированного) значения фазы, поэтому v_p называют фазовой скоростью. Продифференцировав уравнение (3) получим, что

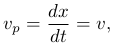
т.е. скорость распространения волны v в (2), есть скорость перемещения фазы v_p. В (2) dx/dt ≥ 0 следовательно, волна распространяется в сторону увеличения x. Волна, распространяющаяся в обратном направлении, записывается как

Ψ = a cos [ω(t+x/v)+α].

Определим важные для дальнейшего применения величины:

длина волны λ = v T = 2 π v / ω = v / ν, ν — частота (линейная) колебаний ν =ω / (2π);
волновое число k = ω/v = 2π T / v = 2π / λ.

В этих обозначениях уравнение (2) можно записать как

Ψ = a cos(ω t - k r + α).

Если волна распространяется в произвольном направлении, то уравнение плоской волны записывается как

Ψ = a cos(ω t - k r).

Здесь α=0 и k = (ω/v)n — волновой вектор, направление которого совпадает с направлением распространения волны (n — единичный вектор в направлении распространения волны).

Для сферических волн, распространяющихся в однородной, изотропной среде, продольная волна имеет вид

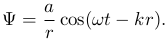
Здесь r — расстояние от точечного источника волны, до точки наблюдения.