Числовые характеристики двумерной случайной величиной

Ковариация и коэффициент корреляции случайных величин

Пусть (X₁, X₂) — двумерный случайный вектор.

Определение. Ковариацией (корреляционным моментом) cov(X₁, X₂) случайных величин X₁ и X₂ называют математическое ожидание произведения случайных величин 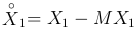и :

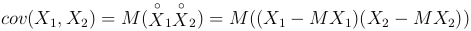
Формулы, определяющие ковариацию:

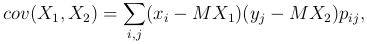
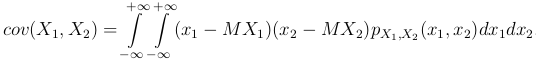
для дискретных случайных величин X₁ и X₂
для непрерывных случайных величин X₁ и X₂

Понятие ковариации позволяет записать выражение для дисперсии суммы произвольных (а не только независимых) случайных величин:

D(X+Y) = DX + DY + 2 cov(X, Y).

Теорема. Ковариация имеет следующие свойства

1. cov(X, X)=DX.
2. cov(X₁, X₂)=0 для независимых случайных величин X₁ и X₂.
3. Если Y_i=a_iX_i+b_i, i=1,2, то
cov(Y₁, Y₂)=a₁a₂cov(X₁, X₂).
4. .
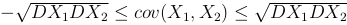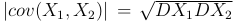5. тогда и только тогда, когда случайные величины X₁ и X₂ связаны линейной зависимостью, т.е. существуют такие числа a и b, при которых
X₂=aX₁-b.
6. cov(X₁, X₂)=M(X₁, X₂) - MX₁ MX₂.

Пример. Пусть случайная величина X имеет равномерное в интервале (-1, 1) распределение, а случайная величина Y связана со случайной величиной X функциональной зависимостью Y=X².

Поскольку MX=0, по 6 свойству ковариации имеем:

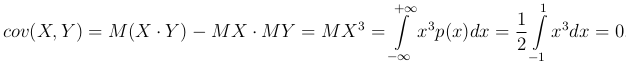
Таким образом из линейной зависимость случайных величин не следует, что их ковариация равна нулю.

Определение. Случайные величины X и Y называют некоррелированными, если их ковариация равна нулю, т.е.

cov(X₁, X₂)=0.

Итак, из коррелированности случайных величин не следует их независимость.

Определение. Коэффициентом корреляции случайных величин X и Y называют число ρ=ρ(X, Y), определяемое равенством

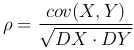
При этом предполагается, что DX>0 и DY>0.

Теорема. Коэффициент корреляции имеет следующие свойства.

1. ρ(X,X)=1.
2. Если случайные величины X и Y являются независимыми (и существуют DX > 0 и DY > 0), то ρ(X, Y)=0.
3. ρ(a₁X₁+b₁, a₂X₂+b₂)=± ρ(X₁, X₂). При этом знак плюс нужно брать в том случае, когда a₁ и a₂ имеют одинаковые знаки, и минус — в противном случае.
4. -1≤ ρ(X, Y)≤ 1.
5. |ρ(X,Y)|=1 тогда и только тогда, когда случайные величины X и Y связаны линейной зависимостью.