Двумерная случайная величина

Совместная функция распределения

Определение. Совокупность двух случайных величин

X₁=X₁(ω), X₂=X₂(ω),

заданных на одном и том же вероятностном пространстве, называют двумерной случайной величиной или двумерным случайным вектором. При этом сами случайные величины X₁, X₂ называют координатами случайного вектора.

Обозначения: (X₁, X₂), 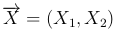, (X, Y).

Пример. Отклонение точки разрыва снаряда от точки прицеливания при стрельбе по плоской цели можно задать двумерной случайной величиной (X, Y), где X — отклонение по дальности, Y — отклонение в боковом направлении.

Определение. Функцией распределения (вероятностей)

F(x, y) = F_X,Y(x, y)

двумерного случайного вектора (X, Y) называют функцию, значение которой в точке (x,y)∈ R² равно вероятности совместного осуществления (пересечения) событий {X < x}, {Y < y}, т.е.

F(x, y) = F_X,Y(x, y) = P{X < x, Y < y}.

Функцию распределения F(x, y) называют также совместной двумерной функцией распределения случайных величин X, Y.

Значение двумерной функции распределения в точке (a₁, a₂) представляет собой вероятность попадания точки с координатами (X₁, X₂) в квадрант с вершиной в точке (a₁, a₂), заштрихованный на рисунке~1.

Теорема. Двумерная функция распределения удовлетворяет следующим свойствам:

1. 0 ≤ F(x₁, x₂) ≤ 1;
2. F(x₁, x₂) — неубывающая функция по каждому из аргументов x₁ и x₂;
3. F(-∞, x₂) = F(x₁, -∞) = 0;
4. F(+∞, +∞) = 1;
5. P{a₁ ≤ X₁ < b₁, a₂ ≤ X₂ < b₂} = F(b₁, b₂) - F(b₁, a₂) - F(a₁, b₂) + F(a₁, a₂);
6. F(x₁, x₂) — непрерывная слева в любой точке (x₁,x₂)∈ R² по каждому из аргументов x₁ и x₂ функция;
7. F_X₁,X₂(x, +∞) = F_X₁ (x),F_X₁,X₂(+∞, x) = F_X₂ (x).

Дискретные двумерные случайные величины

Определение. Двумерную случайную величину (X,Y) называют дискретной, если каждая из случайных величин X и Y является дискретной.

Пусть дискретная величина X принимает только значения x₁, …, x_n, Y — значения y₁, …, y_m, а координаты двумерного вектора (X, Y) — пары значений (x_i, y_i), i=1, 2, …, n, j=1, 2, …, m. Распределение двумерной дискретной случайной величины удобно представить в виде таблицы.

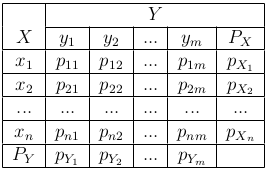
Здесь p_ij = P{X=x_i, Y=y_j} — вероятность совместного осуществления событий {X=x_i} и {Y=y_j}. В этой таблице обычно добавляют одну строку «P_Y» и столбец «P_X». На пересечении столбца «P_X» со строкой «x_i» записывают число

p_{X_i} = p_i1 + … + p_im.

С другой стороны,

p_{X_i} = P{X=x_i},

т.е. вероятность того, что случайная величина X примет значение x_i. Таким образом, первый и последний столбцы таблицы дают нам ряд распределения случайной величины X.

Аналогично, в последней строке «P_Y» помещены значения

p_{Y_j} = p_1j + … + p_nj,

а первая и последняя строки дают ряд распределения случайной величины Y.

Для контроля правильности составления таблицы рекомендуется просуммировать элементы последней строки и последнего столбца. Если хотя бы одна из этих сумм не будет равна единице, то при составлении таблицы была допущена ошибка.

Для того, чтобы определить совместную функцию распределения F_X,Y(x, y) необходимо просуммировать p_ij по всем значения i и j, для которых x_i < x, y_j < y, т.е.

Непрерывные случайные величины

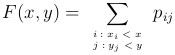
Определение. Непрерывной двумерной случайной величиной (X, Y) называют такую двумерную случайную величину (X, Y), совместную функцию распределения которой

F(x₁, x₂) = P{X < x₁, Y < x₂}

можно представить в виде сходящегося несобственного интеграла:

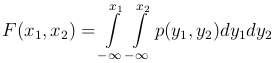
Функцию p(x₁, x₂) = p_X,Y(x₁, x₂) называют совместной плотностью распределения случайных величин X и Y или плотностью распределения случайного вектора (X, Y).

Двойной интеграл можно представить в виде повторного

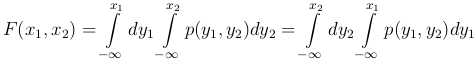
Если p(x₁, x₂) непрерывная функция по обоим аргументам, то

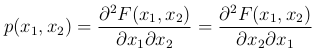
Теорема. Двумерная плотность распределения обладает следующими свойствами:

1. p(x₁, x₂) ≥ 0.
2. .
3. .
4. P{x₁ < X < x₁+Δ x₁, x₂ < Y < x₂+Δ x₂} ≈ p(x₁, x₂)Δ x₁Δ x₂.
5. P{X=x₁, Y=x₂}=0.
6. .
7. .
8. .

Независимые случайные величины

p>Определение. Случайные величины X и Y называют независимыми, если совместная функция распределения F_X,Y(x, y) является произведением одномерных функций распределения F_X(x) и F_Y(y):

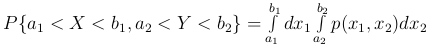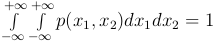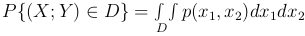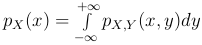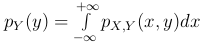F_X,Y(x, y) = F_X(x) F_Y(y).

В противном случае случайные величины называют зависимыми.

Из определения вытекает, что для независимых случайных величин X и Y события {X<x} и {,i>Y<y} являются независимыми.

Теорема. Для того чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы для всех x и y

p_X,Y(x, y) = p_X(x) p_Y(y).

Дискретные случайные величины X и Y являются независимыми тогда и только тогда, когда для всех возможных значений x_i и y_j

p_i,j = P{X=x_i, Y=y_j} = P{X=x_i} P{Y=y_j} = p_{X_i} p_{Y_j}.