Классическое определение вероятности

Определение. Вероятностью события A называют отношение числа N_A благоприятствующих событию A элементарных исходов к общему числу N равновозможных элементарных исходов, то есть

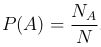
Элементарные исходы в некотором опыте называют равновозможными, если в силу условий проведения опыта можно считать, что ни один из них не является объективно более возможным, чем другие.

Опыт, удовлетворяющий условию равновозможности элементарных исходов, часто называют также классической схемой.

Пример. Из слова «НАУГАД» выбирается наудачу одна буква. Какова вероятность того,что эта буква гласная?

Пусть A — событие заключающееся в том, что в результате опыта выбрана гласная буква. Событию A благоприятствуют три элементарных события: выбраны буквы «А», «А», «У», поэтому m=3. Общее число n всех возможных событий равно количеству букв в слове, n=6. Следовательно P(A)=3/6=1/2.

Пример. Брошены две игральные кости. Вычислить вероятность события A — сумма выпавших очков больше их произведения.

Найдем общее количество элементарных событий n. На выпавшей грани «первой» игральной кости может появиться одно очко, два очка, …, шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Таким образом n=6·6=36. Найдем количество m элементарных событий, благоприятствующих событию A. Выпишем те результаты испытаний, для которых сумма очков больше их произведения. Имеем: (1;1), (1;2), (1;3), (1;4), (1;5), (1;6), (6;1), (5;1), (4;1), (3;1) и (2;1). В результате получим m=11. По классическому определению вероятности: P(A)=11/36.

Свойства вероятностей:

Свойство 1. Для любого события A вероятность удовлетворяет неравенству P(A) ≥ 0.

Свойство 2. Для достоверного события Ω, которое содержит все N элементарных исходов, P(Ω)=1.

Свойство 3. Если события A и B несовместны (AB=∅), то P(A+B)=P(A)+P(B).

Следствие 1. .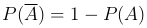

Следствие 2. P(∅)=0.

Следствие 3. P(A) < P(B), если A⊂B.

Недостатки классического определения:

а) оно применимо только к Ω с конечным числом элементов;
б) если Ω конечно, его нельзя применить, если среди исходов есть более предпочтительные или менее предпочтительные.

Вычисление вероятностей с помощью формул комбинаторики

Пример. Из шести карточек, образующих слово «МАСТЕР», наудачу выбирают четыре и выкладывают слева направо. Найти вероятность того, что в результате получится слово «ТЕМА» (событие A).

Элементарным исходом в данном опыте является любая четверка карточек с учетом порядка их выбора, т.е. размещение из n=6 элементов по m=4 элементов. Поэтому число этих исходов равно числу размещений из шести элементов по четыре элемента, т.е.

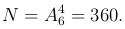
Очевидно, что число исходов, благоприятствующих событию A

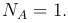
Следовательно,

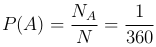
Пример. К Новому году четырем детям были приготовлены подарки. Дед Мороз перепутал подарки и вручил их детям случайным образом. Найти вероятность того, что каждый ребенок получил свой подарок.

В данном случае число элементарных исходов равно числу перестановок из n=4 элементов, т.е.

N = P₄ = 24.

Поскольку число благоприятствующих событию A исходов

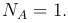
то

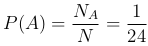
Пример. Из 10 первых букв русского алфавита составлены всевозможные трехбуквенные «слова». Найти вероятность того, что случайно выбранное «слово» окажется «словом» «ИИИ».

Число различных «слов» равно числу размещений с повторениями из 10 элементов по 3 элемента, т.е.

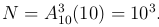
Поскольку благоприятствующий исход только один, то

P(A) = 0.001.

Рассмотрим задачу, часто встречающуюся в приложениях: Пусть имеется n=n₁+…+n_k различных элементов, причем из них n₁ элементов первого типа, n₂ — второго типа, …, n_k — k-го типа. Случайным образом из этих элементов выбираются m элементов. Вероятность события A состоящего в том, что среди выбранных элементов окажется ровно m₁ ≤ n₁ элементов первого типа, m₂ ≤ n₂ элементов второго типа, …, m_k ≤ n_k элементов k-го типа, m₁+…+m_k=m, обозначают P(m₁,…,m_k), и вычисляют по формуле

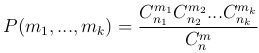
Определение. Рассмотренный способ выбора элементов называют гипергеометрической схемой.

Пример. Из колоды в 36 карт наудачу извлекают 10 карт. Найти вероятность того, что среди выбранных карт окажутся четыре карты пиковой масти, три — трефовой, две — бубновой и одна — червовой.

Воспользуемся гипергеометрической схемой, в которой n=36, n₁=n₂=n₃=n₄=9, m₁=4, m₂=3, m₃=2, m₄=1. Следовательно,