Условная вероятность

Рассмотрим события A и B, связанные с одним и тем же опытом. Пусть из каких-то источников стало известно, что событие B наступило, но неизвестно, какой конкретно из элементарных исходов, составляющих событие B, произошел. Что можно сказать в этом случае о вероятности события A?

Вероятность события A, вычисленную в предположении, что событие B произошло, принято называть условной вероятностью и обозначать P(A|B).

Условную вероятность P(A|B) события A при условии события B в рамках классической схемы вероятности естественно определить как отношение N_AB исходов, благоприятствующих совместному осуществлению событий A и B, к числу N_B исходов, благоприятствующих событию B, то есть

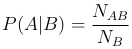
Если поделить числитель и знаменатель этого выражения на общее число N элементарных исходов, то получим

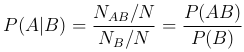
Итак,

Определение. Условной вероятностью события A при условии наступления события B называют отношение вероятности пересечения событий A и B к вероятности события B:

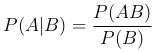
При этом предполагают, что P(B) ≠ 0.

Теорема. Условная вероятность P(A|B) обладает всеми свойствами безусловной вероятности P(A).

Смысл этой теоремы заключается в том, что условная вероятность представляет собой безусловную вероятность, заданную на новом пространстве Ω₁ элементарных исходов, совпадающем с событием B.

Пример. Из урны, в которой a=7 белых и b=3 черных шаров, наугад без возвращения извлекают два шара. Пусть событие A₁ состоит в том, что первый извлеченный шар является белым, а A₂ — белым является второй шар. Требуется найти P(A₂|A₁).

Способ 1.. По определению условной вероятности

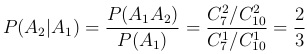
Способ 2.. Перейдем к новому пространству элементарных исходов Ω₁. Так как событие A₁ произошло, то это означает, что в новом пространстве элементарных исходов всего равновозможных исходов N_Ω₁=a+b-1=9, а событию A₂ благоприятствует при этом N_A₂=a-1=6 исходов. Следовательно,

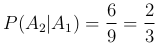
Теорема [умножения вероятностей]. Пусть событие A=A₁A₂…A_n и P(A)>0. Тогда справедливо равенство:

P(A) = P(A₁) P(A₂|A₁) P(A₃|A₁A₂) … P(A_n|A₁A₂…A_n-1).

Замечание. Из свойства коммутативности пересечения можно писать

P(A₁A₂) = P(A₁) P(A₂|A₁)

P(A₁A₂) = P(A₂) P(A₁|A₂).

Пример. На 7 карточках написаны буквы, образующие слово «СОЛОВЕЙ». Карточки перемешивают и из них наугад последовательно извлекают и выкладывают слева направо три карточки. Найти вероятность того, что получится слово «ВОЛ» (событие A).

Пусть событие A₁ — на первой карточке написана буква «В», A₂ — на второй карточке написана буква «О», A₂ — на третьей карточке — буква «Л». Тогда событие A — пересечение событий A₁, A₂, A₃. Следовательно,

P(A) = P(A₁A₂A₃) = P(A₁) P(A₂|A₁) P(A₃|A₁A₂).

P(A₁)=1/7; если событие A₁ произошло, то на оставшихся 6 карточках «О» встречается два раза, значит P(A₂|A₁)=2/6=1/3. Аналогично, P(A₃|A₁)=2/6=1/3. Следовательно,

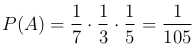
Определение. События A и B, имеющие ненулевую вероятность, называют независимыми, если условная вероятность A при условии B совпадает с безусловной вероятностью A или если условная вероятность B при условии A совпадает с безусловной вероятностью B, то есть

P(A|B) = P(A) или P(B|A) = P(B),

в противном случае события A и B называют зависимыми.

Теорема. События A и B, имеющие ненулевую вероятность, являются независимыми тогда и только тогда, когда

P(AB) = P(A) P(B).

Таким образом, можно дать эквивалентное определение:

Определение. События A и B называют независимыми, если P(AB) = P(A) P(B).

Пример. Из колоды карт, содержащей n=36 карт, наугад извлекают одну карту. Обозначим через A событие, соответствующее тому, что извлеченная карта будет пиковой, а B — событие, соответствующее появлению «дамы». Определим являются ли зависимыми события A и B.

P(A)=9/36=1/4, P(B)=4/36=19, P(AB)=1/36, 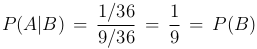. Следовательно, события A и B независимы. Аналогично, .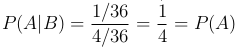