Непрерывные случайные величины

Определение. Непрерывной называют случайную величину X, функцию распределения которой F(x) можно представить в виде

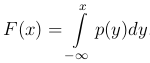
Функцию p(x) называют плотностью распределения (вероятностей) случайной величины X.

Предполагают, что несобственный интеграл сходится.

Функция распределения для непрерывной случайной величины является непрерывной на всей числовой оси и в точках непрерывности плотности распределения p(x) имеет место равенство

p(x)=F′(x),

что следует из свойств интеграла с переменным верхним пределом.

Замечание. Функцию распределения F(x) называют интегральным законом распределения случайной величины, а плотность распределения p(x) — дифференциальным законом распределения той же случайной величины.

Теорема. Плотность распределения обладает следующими свойствами:

1. p(x) ≥ 0;
2. ;
3. ;
4. P{x ≤ X < x+Δ x} ≈ p(x)dx в точках непрерывности плотности распределения;
5. P{X=x}=0 — вероятность попадания в любую точку равна нулю.

Некоторые непрерывные случайные величины

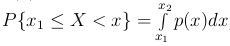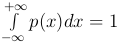Равномерное распределение. Случайная величина имеет равномерное распределение на отрезке [a, b], если ее плотность распределения

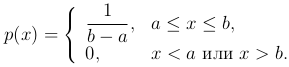
Функция распределения в этом случае определяется выражением

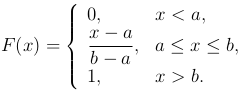
Вероятность попадания равномерно распределенной случайной величины в интервал (x₁, x₂), лежащей внутри отрезка [a, b], равна

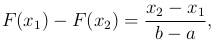
то есть пропорциональна длине этого интервала. Таким образом, равномерное распределение реализует схему геометрической вероятности при бросании точки на отрезок [a, b].

Экспоненциальное распределение. Случайная величина распределена по экспоненциальному (показательному) закону, если она имеет плотность распределения

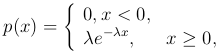
где λ>0 — параметр экспоненциального распределения.

Функция распределения имеет следующее выражение

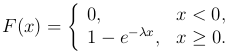
Экспоненциальное распределение тесно связано с распределением Пуассона, а именно: если времена между последовательными наступлениями некоторого события представляют собой независимые экспоненциально распределенные случайные величины, то число наступлений этого события за время t распределено по закону Пуассона с параметром λ t.

Нормальное распределение. Случайная величина распределена по нормальному (или гауссову) закону, если ее плотность

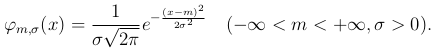
Нормальное распределение зависит от двух параметров: m, называемого математическим ожиданием или средним значением, и σ, называемого средним квадратичным отклонением.

Функция распределения имеет вид:

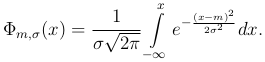
параметр m определяет положение «центра симметрии» плотности нормального распределения, то есть график плотности нормального распределения симметричен относительно прямой x=m, а σ — разброс значений случайной величины относительно центра симметрии.

Если m=0, σ=1, то такой нормальный закон называют стандартным и его функцию распределения обозначают Φ(x), а плотность распределения — φ(x).