Дисперсия. Моменты высших порядков

Две случайные величины могут иметь одинаковые средние значения, но их возможные значения будут по-разному рассеиваться вокруг этого среднего. Например, средний бал на экзамене в двух группах равен «4», но в первой группе почти все получили «4», а во второй группе «4» нет вообще, но есть как «3», так и «5».

Поэтому, наряду со средним значением, хотелось бы иметь и число, характеризующее «разброс» случайной величины относительно своего среднего значения. Такой характеристикой служит дисперсия.

Определение. Вторым начальным моментом m₂ случайной величины X называют математическое ожидание квадрата X (Y(x)=x²):

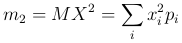
для дискретной случайной величины X и

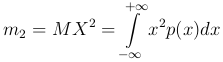
для непрерывной.

Определение. Дисперсией DX случайной величины X называют математическое ожидание квадрата отклонения случайной величины X от ее среднего значения, т.е.

DX = M(X-MX)².

Если в качестве функции случайной величины взять

Y(x) = (x-MX)²,

то получим формулы для дисперсии дискретной

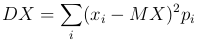
и непрерывной

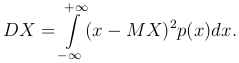
случайной величин.

Определение. Случайную величину

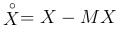
называют центрированной случайной величиной.

Тогда дисперсия DX представляет собой второй момент центрированной случайной величины. Поэтому ее называют иногда вторым центральным моментом случайной величины.

Теорема. Дисперсия удовлетворяет следующим свойствам:

1. Если случайная величина X принимает всего одно значение C с вероятностью единица, то DC=0.
2. D(aX+b)=a²DX.
3. DX=MX²-(MX)².
4. D(X+Y)=DX+DY для независимых случайных величин X и Y.

Нетрудно видеть, что дисперсия DX имеет размерность квадрата размерности случайной величины X. Для практических же целей удобно иметь величину, характеризующую разброс значений случайной величины вокруг ее математического ожидания, размерность которой совпадает с размерностью X. В качестве такой величины используют 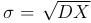, которую называют средним квадратичным отклонением случайной величины X.

Пример. Найдем дисперсию случайной величины X распределенной по закону Пуассона. Для этого воспользуемся свойством 3 дисперсии. Математическое ожидание MX=λ, определим второй момент:

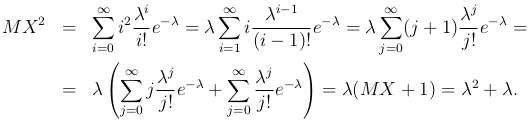
Таким образом,

DX = λ²+λ-λ²=λ.

Пример. Пусть X — число успехов в n испытаниях по схеме Бернулли. Представим X в виде суммы

X = X₁+…+X_n.

Дисперсия каждого слагаемого равна:

DX_i = (0-MX_i)²q + (1-MX_i)²p = (-p)²q + (1-p)²p = p²q+q²p = pq(p+q) = pq.

Учитывая, что случайные величины X_i являются независимыми, в силу свойства 4 дисперсии получаем

DX = DX₁ + … + DX_n = npq.

Пример. Дисперсия равномерно распределенной на отрезке [a, b] случайной величины X определяется формулой

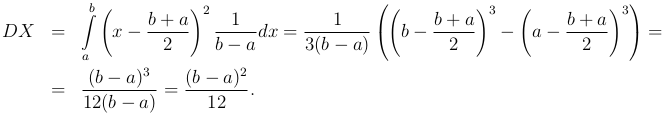
Пример. Дисперсия случайной величины X, распределенной по нормальному закону с параметрами m и σ, имеет вид

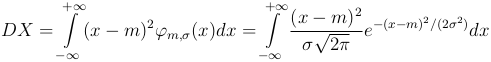
Делая замену y=(x-m)σ, получаем

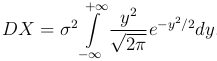
Полагая 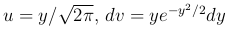и интегрируя по частям, найдем

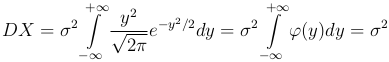
Определение. Моментом k-го порядка m_k случайной величины X называют математическое ожидание k-й степени случайной величины X:

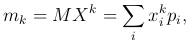
если X — дискретная величина, и

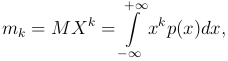
если X — непрерывная случайная величина.

Определение. Центральным моментом k-го порядка 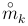случайной величины X называют математическое ожидание k-й степени случайной величины :

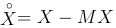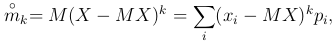
если X — дискретная величина, и

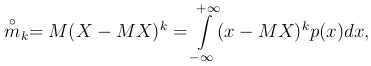
если X — непрерывная случайная величина.