Числовые характеристики случайных величин

Математическое ожидание случайной величины

Определение. Математическим ожидание (средним значением) MX дискретной случайной величины X называют сумму произведений значений x_i случайной величины и вероятностей p_i = P{X=x_i}, с которыми случайная величина принимает значения: 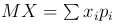. При этом, если множество возможных значений случайной величины X счетно, предполагается, что

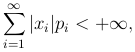
то есть ряд, определяющий математическое ожидание, сходится абсолютно; в противном случае говорят, что математическое ожидание случайной величины X не существует.

Математическое ожидание дискретной случайной величины имеет аналог в теоретической механике. Пусть на прямой расположена система материальных точек с массами p_i (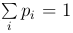) и пусть x_i — координата i-той точки. Тогда центр масс системы будет иметь координату:

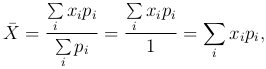
совпадающую с математическим ожиданием MX случайной величины X.

Пример. Пусть X — число угаданных номеров в «Спортлото 6 из 49». В соответствие с рядом распределения имеем

MX = 0 · p₀ + 1 · p₁ + 2 · p₂ + 3 · p₃ + 4 · p₄ + 5 · p₅ + 6 · p₆ ≈
≈ 0 · 0.436 + 1 · 0.413 + 2 · 0.1324 + 3 · 0.0176 + 4 · 0.00097 + 5 · 1.8 · 10^-5 + 6 · 7 · 10^-8 ≈
≈ 0.735.

Таким образом, среднее число угаданных номеров приблизительно равно 0.735.

Пример. Найдем математическое ожидание случайной величины X, распределенной по биномиальному закону (число успехов в n испытаниях по схеме Бернулли с вероятностью успеха p):

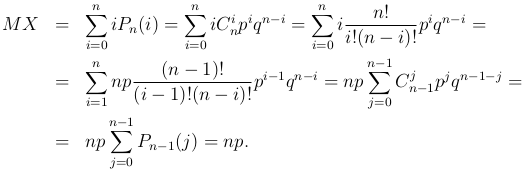
Пример. Пусть случайная величина X имеет распределение Пуассона. Тогда

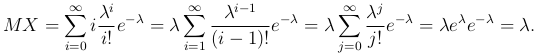
Пример. Найдем математическое ожидание случайной величины X, имеющей геометрическое распределение:

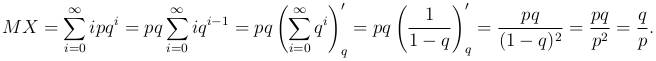
Пример. Положительная целочисленная случайная величина X имеет закон распределения, задаваемый выражением

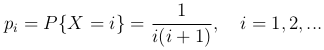
Тогда

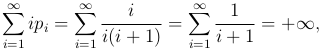
следовательно, математическое ожидание случайной величины X не существует.

Определение. Математическом ожиданием (средним значением) MX непрерывной случайной величины называют интеграл

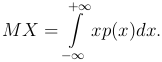
Предполагается, что

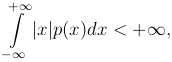
то есть несобственный интеграл, определяющий математическое ожидание, сходится абсолютно.

Математическое ожидание непрерывной случайной величины можно интерпретировать как центр масс стержня, плотность массы которого в точке x равен p(x).

Пример. Найдем математическое ожидание равномерно распределенной на отрезке [a, b] случайной величины X. Поскольку в этом случае p(x)=0 при x < a и x > b, то

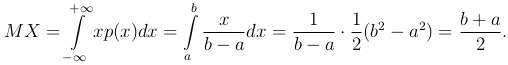
Итак, MX совпадает с серединой отрезка [a, b].

Пример. Найдем математическое ожидание случайной величины X, распределенной по нормальному закону с параметрами m и σ:

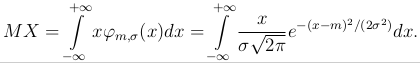
Делая замену y=(x-m)/σ, получаем

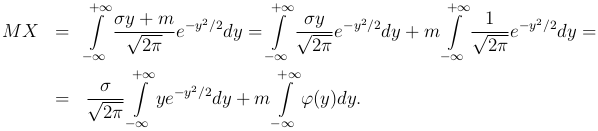
Первый интеграл равен 0 в силу нечетности подынтегральной функции, а второй интеграл равен 1, как интеграл от стандартной нормальной плотности.

Таким образом, MX=m, то есть параметр m имеет смысл математического ожидания случайной величины X.

Пример. Случайная величина X распределение с плотностью (распределение Коши):

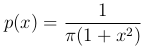
Тогда 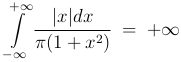, так как подынтегральная функция эквивалентна 1/(πx) при x→+∞. Поэтому математическое ожидание случайной величины X не существует.