Функции от случайных величин

Пусть в пространстве элементарных исходов Ω с определенной вероятностью P задана случайная величина X=X(ω). Рассмотрим действительную функцию y=Y(x) действительного аргумента x (область определения которой включает в себя множество возможных значений случайной величины X.

Определение. Случайную величину Y, которая каждому элементарному исходу ω ставит в соответствие число Y(ω)=Y(X(ω)), называют функцией Y(X) (скалярной) от скалярной случайной величины X.

Функция Y=Y(X) от дискретной случайной величины также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина X.

Если случайная величина X имеет ряд распределения, представленный в таблице 1, то ряд распределения случайной величины Y=Y(X) определяется таблицей 2.

При этом, если в верхней строке таблицы 2 появляются одинаковые значения Y(x_i), соответствующие столбцы нужно объединить в один, приписав им суммарную вероятность.

Пример. Рассмотрим игру «Спортлото 6 из 49». Поставив на некоторые фиксированные номера, мы в результате розыгрыша получим случайную величину X — число угаданных номеров. Вероятность угадать i номеров (i={0, 1, …, 6}) определяется формулой

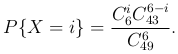
Проводя вычисления, получаем ряд распределения случайной величины X:

Однако случайная величина X нас не интересует, для нас важен выигрыш, связанный с числом угаданных номеров X. Рассмотрим идеализированный вариант игры, при котором не угадав ни одного или угадав один или два номера мы проигрываем (с учетом платы за билет) 0.3 р., угадав три номера получаем выигрыш 2.7 р., угадав 4 номера — 54.7 р., 5 номеров — 699.7 р. и 6 номеров — 9999.7 р. Выигрыш Y зависит только лишь от числа угаданных номеров, то есть представляет собой функцию от случайной величины X:

Y = Y(X).

При этом числовая функция Y(x) определена формулами: Y(0)=Y(1)=Y(2)=-0.3; Y(3)=2.7; Y(4)=54.7; Y(5)=699.7; y(6)=9999.7.

Ряд распределения случайной величины Y получаем из ряда распределения X заменой в верхней строке чисел i=0, 1, …, 6 на соответствующие значения Y(i).

Заметим, что три первых столбца имеют одинаковые значения Y, равные -0.3. Объединяя их в один, окончательно получаем ряд распределения случайной величины Y, представленной в таблице:

Реально при игре в «Спортлото» выигрыш Y зависит от числа играющих, поставивших на ту или иную комбинацию, и в этом случае его нельзя считать функцией от числа угаданных номеров X, а необходимо рассматривать более сложную модель, учитывающую вероятности использования различных комбинаций номеров.

Функция Y=Y(X) от непрерывной случайной величины X может быть как непрерывной, так и дискретной (если, например, множество значений функции Y(X) конечное или счетное).

Найдем функцию распределения F_Y(y) по заданной плотности распределения p_X(y). По самому определению, F_Y(y) представляет собой вероятность события {Y < y}, состоящего из тех элементарных исходов ω, для которых Y(X(ω)) < y. В свою очередь, вероятность события {Y(X(ω)) < y} можно определить, используя аксиому сложения вероятностей, «просуммировав» вероятности всех возможных значений X(ω) случайной величины X, для которых Y(X) < x. Поскольку, как мы знаем, вероятность случайной величине X принять значение в промежутке от x до x+Δ x приближенно равна p_X(x)dx, то заменяя сумму на интеграл, получаем

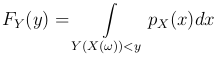
Последняя запись означает, что интегрирование проводится по всем тем значениям x, для которых Y(x) < y.

Таким образом, данная формула позволяет вычислить функцию распределения F_Y(y) случайной величины Y(X) через плотность p_X(x) распределения случайной величины X.

Пример. Случайная величина X имеет стандартное нормальное распределение. Найдем распределение случайной величины Y=X². В данном случае Y(x)=x², поэтому

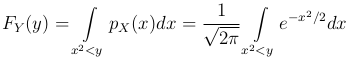
Поскольку при y ≤ 0 нет ни одного значения x, для которого x² < y, то не существует ни одного ω, для которого Y(X(ω))=(X(ω))², и F_Y(y)=0 при y ≤ 0.

Если же y > 0, то область {x² < y} совпадает с областью 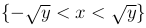, и, значит,

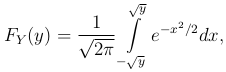
или в силу четности подынтегральной функции

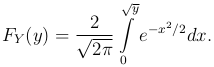
Делая в последнем интеграле замну z=x² при y > 0, получаем

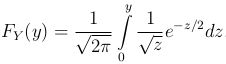
Следовательно,

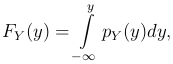
где