Предельные теоремы теории вероятностей

Неравенства Чебышева. Закон больших чисел

Теорема. Для каждой неотрицательной случайной величины X, имеющей математическое ожидание MX, при любом ε > 0 справедливо соотношение

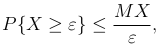
называемое первым неравенством Чебышева.

Пример. Пусть X — время опоздания студента на лекцию, причем известно, что MX=1 мин. Воспользовавшись первым неравенством Чебышева, оценим вероятность P{X≥ 5} того, что студент опоздает не менее, чем на 5~мин.

Имеем

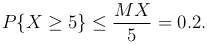
Таким образом, искомая вероятность не более 0.2, т.е. в среднем из каждых пяти студентов опаздывает, по крайней мере, на 5 минут не более чем один студент.

Теорема. Для каждой случайной величины X, имеющей дисперсию DX=σ², при любом ε > 0 справедливо второе неравенство Чебышева

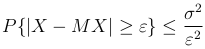
Пример. Пусть в условиях предыдущего примера известно что 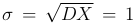. Оценим минимальное значение x₀, при котором вероятность опоздания студента на время не менее x₀ не превышает заданного значения P_*=0.1.

Воспользуемся вторым неравенством Чебышева:

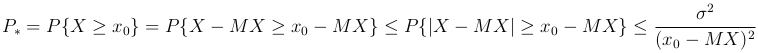
Значит

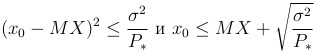
Получим:

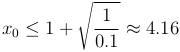
Таким образом, вероятность опоздания студента на время более 4.16 мин не более 0.1.

Пусть X₁, X₂, …, X_n, … — последовательность случайных величин, имеющих математические ожидания m_i=MX_i.

Определение. Последовательность X₁, X₂, …, X_n, … случайных величин удовлетворяет закону больших чисел (слабому), если для любого ε > 0

Другими словами: при большом числе испытаний средние арифметические случайных величин практически перестают быть случайными и совпадают со своими средними значениями.

Теорема [закон больших чисел в форме Чебышева]. Если последовательность X₁, X₂, …, X_n, … независимых случайных величин такова, что существуют MX_i=m_i и DX_i=σ_i², причем дисперсии σ_i² ограничены в совокупности (т.е. σ_i²≤ C < +∞), то для последовательности X₁, X₂, …, X_n, … выполнен закон больших чисел.

Теорема [закон больших чисел в форме Бернулли]. Пусть проводится n испытаний по схеме Бернулли и Y_n — общее число успехов в n испытаниях. Тогда наблюдаемая частота успехов

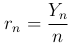
сходится по вероятности к вероятности p успеха в одном испытании, т.е. для любого ε > 0

P{|r_n-p|≥ε} → 0 при n→∞.

Центральная предельная теорема

Теорема [центральная предельная теорема]. Пусть X₁, X₂, …, X_n, … — последовательность независимых одинаково распределенных случайных величин, MX_n=m, DX_n=σ². Тогда

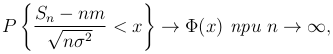
где Φ(x) — функция стандартного нормального распределения.

Следствие из центральной предельной теоремы:

Теорема [интегральная теорема Муавра—Лапласа]. Обозначим S_n — суммарное число успехов в n испытаниях по схеме Бернулли с вероятностью успеха p и вероятностью неудачи q=1-p. Тогда с ростом n последовательность функции распределения случайных величин 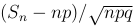сходится к функции стандартного нормального распределения, т.е.

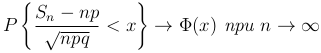
Пример. Для определения скорости v движения объекта делают n измерений v₁, …, v_n, причем i-е измерение проводят с погрешностью X_i (т.е. v_i=v+X_i), при этом погрешности измерений являются независимыми и одинаково распределенными случайными величинами с математическим ожиданием MX_i=0 (отсутствуют системтическими погрешности наблюдений) и дисперсии DX_i=σ².

Оценим вероятность того, что средняя наблюдаемая скорость

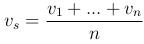
будет отличаться от истинной скорости v не более чем на ε. Имеем

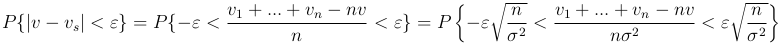
Считая, что число n измерений велико, воспользуемся центральной предельной теоремой, согласно которой случайная величина

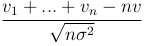
приближенно распределена по стандартному нормальному закону. Значит