Геометрическое и аксиоматическое определение вероятности

Геометрическое определение вероятности

Геометрическое определение вероятности обобщает классическое на случай бесконечного множества элементарных исходов Ω тогда, когда Ω представляет собой подмножество пространства R (числовая прямая), R² (плоскость), Rⁿ (n-мерное евклидовое пространство).

Под мерой μ(A) подмножества A будем понимать его длину, площадь или объем (обобщенный объем) в зависимости от того, какому пространству принадлежит Ω: в R, в R² или в R³ (Rⁿ). Будем считать, что пространство Ω имеет конечную меру, а вероятность попадания «случайно брошенной» точки в любое подмножество Ω пропорциональна мере этого подмножества и не зависит от его расположения и формы. В этом случае говорят, что рассматривается «геометрическая схема» или «точку наугад бросают в область Ω».

Определение. Вероятностью события A называют число P(A), равное отношению меры множества A к мере множества Ω:

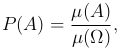
где μ(A) — мера множества A.

Замечание 1. Геометрическая вероятность сохраняет отмеченные ранее свойства вероятности P(A) в условиях классической схемы.

Пример. На бесконечную шахматную доску со стороной квадрата a наудачу бросают монету радиуса r, r < a/2. Найти вероятность того, что монета попадет целиком внутрь одного квадрата.

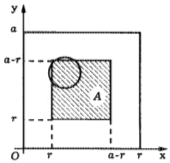
Рис. 1

Пусть (x; y) — координаты центра упавшей монеты. В силу бесконечности шахматной доски можно считать, что элементарные исходы данного эксперимента полностью определяются положением центра упавшей монеты относительно вершин квадрата, содержащего этот центр. Помещая начало координат в одну из вершин указанного квадрата (рис. 1), можно записать множество элементарных исходов в виде

Ω = {(x; y): 0≤ x≤ a, 0≤ y≤ a}.

Область A, соответствующая рассматриваемому событию, имеет вид

A = {(x; y): r≤ x≤ a-r, r≤ y≤ a-r},

т.е является квадратом со стороной a-2r. В соответствии с формулой геометрической вероятности находим

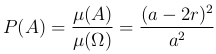
Аксиоматическое определение вероятности

Определение. Пусть каждому событию A поставлено в соответствие число P(A). Числовую функцию P называют вероятностью (или вероятностной мерой), если если она удовлетворяет следующим аксиомам:

Аксиома 1 (аксиома неотрицательности). P(A) ≥ 0;
Аксиома 2 (аксиома нормированности). P(Ω)=1;
Аксиома 3 (расширенная аксиома сложения). для любых попарно несовместных событий A₁, …, A_n, … справедливо равенство:
P(A₁+A₂+…+A_n+…) = P(A₁) + P(A₂) + … + P(A_n) + …

Значение P(A) называют вероятностью события A.

Замечание. Если пространство элементарных исходов Ω является конечным или счетным множеством, то каждому элементарному исходу ω_i ∈ Ω (i=1, 2, …), можно поставить в соответствие число P(ω_i)=p_i ≥ 0 так, что

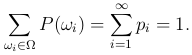
Тогда для любого события A⊂Ω в силу аксиомы 3 вероятность P(A) равна сумме вероятностей P(ω_i) всех тех элементарных исходов, которые входят в событие A, то есть

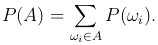
Таким образом, мы определили вероятность любого события, используя вероятности элементарных исходов.

Теорема. Вероятность удовлетворяет следующим свойствам:

1. Вероятность противоположного события .
2. Вероятность невозможного события P(∅)=0.
3. Если A⊂B, то P(A) ≤ P(B) («большему» событию соответствует большая вероятность).
4. Вероятность заключена между 0 и 1: 0 ≤ P(A) ≤ 1.
5. Вероятность объединения двух событий P(A+B) = P(A) + P(B) - P(AB).
6. Вероятность объединения любого конечного числа событий
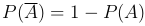P(A₁ ∪ … ∪ A_n) =
P(A₁) + … + P(A_n) - P(A₁A₂) - P(A₁A₃) - … - P(A_n-1A_n) +
+& P(A₁A₂A₃) + … + (-1)ⁿ⁺¹P(A₁A₂…A_n).

Замечание. Утверждения 5 и 6 называются теоремами сложения вероятностей для двух и для n событий соответственно.

Пример (того, что если не учитывать совместность событий, то можно прийти к неправильному результату). Опыт состоит в двукратном подбрасывании монеты. Найдем вероятность события A, означающее появление «герба» хотя бы один раз. Обозначим через A_i — появление «герба» при i-том подбрасывании (i=1, 2). Ясно, что A = A₁ ∪ A₂, и в соответствии с классической схемой вероятности P(A₁)=P(A₂)=1/2. Если не учитывать, что A₁ и A₂ — совместные события, то можно получить «результат»: P(A)=P(A₁)+P(A₂)=1, что неверно, так как ясно, что событие A не является достоверным. Применяя теорему сложения для двух совместных событий и учитывая равенство P(A₁A₂)=1/4, находим P(A)=P(A₁)+P(A₂)-P(A₁A₂)=3/4.