 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика
 Предмет теории вероятностей
Предмет теории вероятностей
Теория вероятностей является разделом математики, в котором изучают математические модели случайных экспериментов, то есть экспериментов, исходы которых нельзя определить однозначно условиями проведения данного опыта.
Так, например, мы не можем предсказать, какой стороной упадет подброшенная монета, сколько очков выпадет на игральной кости, сколько времени проработает электрическая лампочка.
При этом предполагается, что сам эксперимент может быть повторен с первоначальным комплексом исходных данных (хотя бы теоретически) бесконечное число раз.
Например, какая будет погода 1 декабря 2020 года мы не будем знать до этого дня, а после наступления 1 декабря 2020 года она будет полностью определена. Здесь нет возможности повторить испытание. И вопросом погоды 1 декабря 2020 года до этого занимается метеорология, а после — история, но никак не теория вероятностей.
Кроме того необходимо предположить невозможность точного предсказания результатов не только первого испытания, но и каждого последующего.
Например, выяснив номер телефона знакомого, мы сколько бы раз его ни спрашивали, новых цифр не добьемся. Также определив исход химической реакции, а затем проведя ее снова при тех же условиях, мы нового вещества не получим.
Определение. Элементарным исходом (или элементарным событием) называют любой простейший (то есть неделимый в рамках данного опыта) исход опыта. Множество всех элементарных исходов будем называть пространством элементарных исходов.
Другими словами, множество исходов опыта образует пространство элементарных исходов, если выполнены следующие требования:
Обозначим пространство элементарных исходов за Ω, а элементарные исходы: ω1, ωi и т.п.
Таким образом, Ω = {ω1, ω2,…, ωn, …} или Ω = {ωi, i=1, 2, …, n, …}.
Пример. Пусть опыт состоит в однократном подбрасывании монеты. При математическом описании этого опыта возможны только два элементарных исхода: выпадение «герба» (Г, ωГ или ω1) и выпадение «цифры» (Ц, ωЦ или ω2). Таким образом, Ω={Г, Ц}, Ω={ωГ, ωЦ} или Ω={ω1, ω2}.
При двукратном подбрасывании монеты пространство элементарных исходов будет содержать четыре элемента, то есть Ω={ωГГ, ωГЦ, ωЦГ, ωЦЦ}, где ωГГ — появление «герба» и при первом, и при втором подбрасываниях и т.д.
Определение. Любой набор элементарных исходов или, другими словами, произвольное подмножество пространства элементарных исходов, называют событием.
Элементарные исходы, которые являются элементами рассматриваемого подмножества, называют элементарными исходами, благоприятствующими данному событию, или образующими это событие. Обозначаются: A, B1, Ci, …
Пример. При однократном бросании игральной кости имеем Ω={ωi, i=1, …, 6}, где ωi — элементарный исход, заключающийся в выпадении i очков. Рассмотрим следующие события: A — выпадение четного числа очков; B — выпадение нечетного числа очков; C — выпадение числа очков, кратного трем. Тогда
Определение. Событие, состоящее из всех элементарных исходов, то есть событие, которое обязательно происходит в данном опыте, называют достоверным событием.
Обозначение: Ω.
Определение. Событие, не содержащее ни одного элементарного исхода, то есть событие, которое никогда не происходит в данном опыте, называют невозможным событием.
Обозначение: ∅.
Пример. При бросании игральной кости достоверное событие можно описать, например, как выпадение хотя бы одного очка, а невозможное — как выпадение 7 очков.
Определение. Пересечением (произведением) двух событий A и B называют событие C, происходящее тогда и только тогда, когда одновременно происходят оба события A и B, то есть событие, состоящее из тех и только тех элементарных исходов, которые принадлежат и событию A, и событию B.
Обозначение: C=A ∩ B, C=AB.
Определение. События A и B называют несовместными или непересекающимися, если их пересечение является невозможным событием, то есть A ∩ B = ∅. В противном случае события называются совместными или пересекающимися.
Определение. Объединением (суммой) двух событий A и B называют событие C, происходящее тогда и только тогда, когда происходит хотя бы одно из событий A и B, то есть событие, состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из подмножеств A или B.
Обозначение: C=A ∪ B, C=A+B.
Определение. Разностью двух событий A и B называют событие C, происходящее тогда и только тогда, когда происходит событие A, но не происходит событие B, то есть событие, состоящее из тех элементарных исходов, которые принадлежат событию A, но не принадлежат событию B.
Обозначение: C=A\B.
Определение. Дополнением события A (обозначается 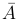 ) называют событие, происходящее тогда и только тогда, когда не происходит событие A, то есть
) называют событие, происходящее тогда и только тогда, когда не происходит событие A, то есть
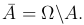
Событие 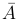 называют также событием, противоположным событию A.
называют также событием, противоположным событию A.
Определение. Событие A включено в событие B (A ⊂ B), если появление события A обязательно влечет за собой наступление события B, или каждый элементарный исходов ω, принадлежащий A, обязательно принадлежит и событию B.
Включение A ⊂ B эквивалентно равенству AB=A.
Пример. Рассмотрим техническое устройство (ТУ), состоящее из m элементов. В теории надежности принято говорить, что элементы соединены последовательно, если ТУ прекращает функционировать при отказе любого элемента, и соединены параллельно, если прекращение функционирования ТУ наступает только при отказе всех m элементов.
Обозначим A — событие, означающее отказ ТУ, а Ai — событие, означающее отказ i-го элемента (i=1, 2, …, m). Тогда события A и Ai связаны соотношениями:
Очевидно, что при параллельном соединении элементов событие A включено в каждое событие Ai, i=1, 2, …, m}, а при последовательно соединении, наоборот, любое событие Ai, i=1, 2, …, m, включено в событие A.
Свойства операций над событиями:
A∪ B=B∪ A, AB=BA.
(A∪ B)∪ C=A∪(B∪ C), (AB)C=A(BC).
(A∪ B)C=AC∪ BC.
(A B)∪ C=(A∪ C)(B∪ C).
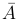 в
в 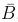 , т.е.
, т.е.
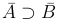
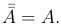
A∪A=AA=A.
