Случайные величины

Определение. Случайной величиной называется числовая величина, значение которой зависит от того, какой именно элементарный исход произошел в результате эксперимента со случайным исходом. Множество всех значений, которые случайная величина может принимать, называют множеством возможных значений этой случайной величины.

Случайные величины обозначают: X, Y₁, Z_i; ξ, η₁, μ_i, а их возможные значения — x₃, y_1k, z_ij.

Пример. В опыте с однократным бросанием игральной кости случайной величины является число X выпавших очков. Множество возможных значений случайной величины X имеет вид

{x₁=1, x₂=2, …, x₆=6}.

Имеем следующее соответствие между элементарными исходами ω и значениями случайной величины X:

То есть каждому элементарному исходу ω_i, i=1, …, 6, ставится в соответствие число i.

Пример. Монету подбрасывают до первого появления «герба». В этом опыте можно ввести, например, такие случайные величины: X — число бросаний до первого появления «герба» с множеством возможных значений {1, 2, 3, …} и Y — число «цифр», выпавших до первого появления «герба», с множеством возможных значений {0, 1, 2, …} (ясно, что X=Y+1). В данном опыте пространство элементарных исходов Ω можно отождествить с множеством

{Г, ЦГ, ЦЦГ, …, Ц…ЦГ, …},

причем элементарному исходу {Ц … ЦГ} ставится в соответствие число m+1 или m, где m — число повторений буквы «Ц».

Определение. Скалярную функцию X(ω), заданную на пространстве элементарных исходов, называют случайной величиной, если для любого x∈ R {ω:X(ω) < x} является событием.

Функция распределения случайной величины

Для исследования вероятностных свойств случайной величины необходимо знать правило, позволяющее находить вероятность того, что случайная величина примет значение из подмножества ее значений. Любое такое правило называют законом распределения вероятностей или распределением случайной величины.

Общим законом распределения, присущим всем случайным величинам, является функция распределения.

Определение. Функция распределения (вероятностей) случайной величины X называют функцию F(x), значение которой в точке x равно вероятности события {X < x}, то есть события, состоящего из тех и только тех элементарных исходов ω, для которых X(ω) < x:

F(x) = P{X < x}.

Обычно говорят, что значение функции распределения в точке x равно вероятности того, что случайная величина X примет значение, меньшее x.

Теорема. Функция распределения удовлетворяет следующим свойствам:

1. 0 ≤ F(x) ≤ 1;
2. F(x₁) ≤ F(x₂) при x₁ < x₂ (F(x) — неубывающая функция);
3. ;
4. P{x₁ ≤ X < x₂} = F(x₂)-F(x₁);
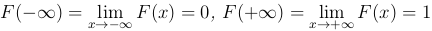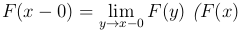5. F(x)=F(x-0), где (F(x) —непрерывная слева функция).

Типичный вид функции распределения.

Дискретные случайные величины

Определение. Случайную величину X называют дискретной, если множество ее возможных значений конечно или счетно.

Определение. Рядом распределения (вероятностей) дискретной случайной величины X называют таблицу, состоящую из двух строк: в верхней строке перечислены все возможные значения случайной величины, а в нижней — вероятности p_i=P\{X=x_i\} того, что случайная величина примет эти значения.

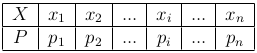
Для проверки правильности составления таблицы рекомендуется просуммировать вероятности p_i. В силу аксиомы нормированности:

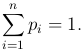
По ряду распределения дискретной случайной величины можно построить ее функцию распределения F(x). Пусть X — дискретная случайная величина, заданная своим рядом распределения, причем x₁ < x₂ < … < x_n. Тогда для всех x ≤ x₁ событие {X < x} является невозможным, следовательно, по определению F(x)=0. Если x₁ < x≤ x₂, то событие {X < x} состоит из тех и только тех элементарных исходов, для которых X(ω)=x₁. Следовательно, F(x)=p₁. Аналогично, при x₂ < x ≤ x₃ событие {X < x} состоит из элементарных исходов ω, для которых либо X(ω)=x₁, либо X(ω)=x₂, то есть {X < x}={X=x₁}+{X=x₂}. Следовательно, F(x)=p₁+p₂ и т.д. При x > x_n событие {X < x} достоверно, тогда F(x)=1.

Закон распределения дискретной случайной величины можно задать также аналитически в виде некоторой формулы или графически. Например, распределение игральной кости описывается формулой

P{X=i} = 1/6, i=1, 2, …, 6.

Некоторые дискретные случайные величины

Биномиальное распределение. Дискретная случайная величина X распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n в соответствии с распределением, заданным формулой Бернулли:

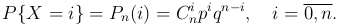
Это распределение является не чем иным, как распределения числа успехов X в n испытаниях по схеме Бернулли с вероятностью успеха p и неудачи q=1-p.

Распределение Пуассона. Дискретная случайная величина X распределена по закону Пуассона, если она принимает целые неотрицательные значения с вероятностями

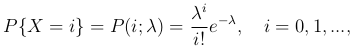
где λ > 0 — параметр распределения Пуассона.

Распределение Пуассона также называют законом редких событий, так как оно всегда проявляется там, где производится большое число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событий.

В соответствие с законом Пуассона распределены, например, число вызовов, поступивших в течение суток на телефонную станцию; число метеоритов, упавших в определенном районе; число распавшихся частиц при радиоактивном распаде вещества.

Геометрическое распределение. Снова рассмотрим схему Бернулли. Пусть X — число испытаний, которое необходимо провести прежде, чем появится первый успех. Тогда X — дискретная случайная величина, принимающая значения 0, 1, 2, …, n, … Определим вероятность события {X=n}.

X=0, если в первом испытании произойдет успех, следовательно, P{X=0}=p.
X=1, если в первом испытании произойдет неудача, а во втором — успех, то P{X=1}=qp.
X=2, если в первых двух испытаниях — неудача, а в третьем — успех, то P{X=2}=q²p.
Продолжая процедуру, получим P{X=i}=qⁱp, i=0, 1, 2, …