Простейшие статистические преобразования

Прежде чем переходить к детальному анализу наблюденных статистических данных, обычно производят их предварительную обработку. Иногда результаты такой обработки уже сами по себе дают наглядную картину исследуемого явления, в большинстве же случаев они служат исходным материалом для получения более подробных статистических выводов.

Вариационный и статистический ряды. Часто бывает удобно пользоваться не самой выборкой X₁, …, X_n, а некоторой ее модификацией, называемой вариационным рядом. Вариационный ряд X₁^*, …, X_n^* представляет собой ту же самую выборку X₁, …, X_n, но расположенную в порядке возрастания элементов: X₁^* ≤ X₂^* ≤ … ≤ X_n^*. Такое преобразование не приводит к потере информации относительно теоретической функции распределения F(x), поскольку, переставив элементы вариационного ряда X₁^*, …, X_n^* в случайном порядке, мы получим новый набор случайных величин X′₁, …, X′_n совместная функция распределения F_{X′₁,…,X′_n}(x₁, …, x_n) которых в точности совпадает с функцией распределения F_{X₁,…,X_n}(x₁, …, x_n) первоначальной выборки X₁, …, X_n.

Если среди элементов выборки X₁, …, X_n (а значит, и среди элементов вариационного ряда X₁^*, …, X_n^*) имеются одинаковые, то наряду с вариационным рядом используют представление выборки в виде статистического ряда (табл. 2), в котором Z₁, …, Z_m представляют собой расположенные в порядке возрастания различные значения элементов выборки X₁, …, X_n, a n₁, …, n_m — числа элементов выборки, значения которых равны соответственно Z₁, …, Z_m.

Статистики. Статистикой S=(S₁, …, S_k) называется произвольная k-мерная функция от выборки X₁, …, X_n:

S₁ = S₁(X₁, …, X_n),
…
S_k = S_k(X₁, …, X_n).

Как функция от случайного вектора (X₁, …, X_n) статистика S также будет случайным вектором, и ее функция распределения

F_{S₁,…,S_k}(x₁, …, x_k) = P{S₁ < x₁, …, S_k < x_k}

определяется для дискретной наблюдаемой случайной величины X формулой

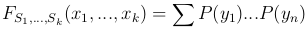
и для непрерывной — формулой

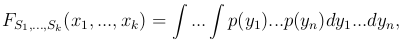
где суммирование и интегрирование производится по всем возможным значениям y₁, …, y_n, для которых выполнена система неравенств S₁(y₁, …, y_n) < x₁, …, S_k(y₁, …, y_n) < x_k.

Статистика S называется достаточной, если она содержит всю ту информацию относительно теоретической функции распределения F(x), что и исходная выборка X₁, …, X_n. В частности, вариационный ряд всегда представляет собой достаточную статистику.

Эмпирическая функция распределения. Эмпирической функцией распределения называют функцию F^*(x), определяющую для каждого значения x относительную частоту события X < x:

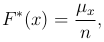
где μ_x — число элементов выборки, значения которых X_i меньше x.

Построение эмпирической функции распределения F^*(x) удобно производить с помощью вариационного ряда X₁^*, …, X_n^*.

Гистограмма, полигон. Для наглядности выборку иногда преобразуют следующим образом. Всю ось абсцисс делят на интервалы (x_i, x_i+1) длиной h_i=x_i+1-x_i и определяют функцию p^*(x), постоянную на i-том интервале и принимающую на этом интервале значение p^*(x)=ν_i/(nh_i), где ν_i — число элементов выборки, попавших в интервал. Функция p_*(x) называется гистограммой.

При наблюдении дискретной случайной величины вместо гистограммы используют полигон частот. Для этого по оси абсцисс откладывают всевозможные значения b₁, …, b_L наблюдаемой величины X, а по оси ординат, пользуясь статистическим рядом, либо числа ν₁, …, ν_L элементов выборки, принявших значения b₁, …, b_L (полигон частот), либо соответствующие наблюденные частоты p₁^*=ν₁/n, …, p_L^*=ν_L/n (полигон относительных частот). Для большей наглядности соседние точки соединяют отрезками прямой.

Выборочные характеристики. Эмпирическая функция распределения F^*(x), построенная по фиксированной выборке X₁, …, X_n, обладает всеми свойствами обычной функции распределения (дискретной случайной величин). В частности по ней можно найти математическое ожидание (выборочное среднее):

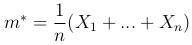
второй момент (выборочный второй момент)

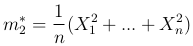
дисперсию (выборочная дисперсия)

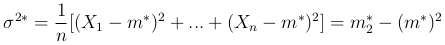
и т.д.