Формула полной вероятности и формула Байеса

Предположим, что в результате опыта может произойти одно из n событий H₁, H₂, …, H_n, которые удовлетворяют следующим условиям:

1) они являются попарно несовместными, то есть H_iH_j=∅ при i ≠ j;
2) хотя бы одно из них должно произойти в результате опыта, другими словами, их объединение есть достоверное событие:
H₁ ∪ H₂ ∪ … ∪ H_n = Ω.
Определение. События H₁, H₂, …, H_n, удовлетворяющие условиям 1 и 2, называют гипотезами.
Замечание. Если события удовлетворяют второму из двух указанных требований, то их совокупность называют полной группой событий. Таким образом, гипотезы — это попарно несовместные события, образующие полную группу событий.
Теорема. Пусть для некоторого события A и гипотез H₁, H₂, …, H_n известны P(H₁), P(H₂), …, P(H_n), которые положительны, и P(A|H₁), P(A|H₂), …, P(A|H_n). Тогда безусловную вероятность определяют по формуле
P(A) = P(H₁) P(A|H₁)+…+P(H_n) P(A|H_n),
которую называют формулой полной вероятности.
Пример. Студент выучил все N=30 экзаменационных билетов, но из них на «пять» — лишь N₁=6. Определить, зависит или нет вероятность извлечения «счастливого» билета (событие A) от того, первым или вторым выбирает студент свой билет.
Рассмотрим две ситуации.
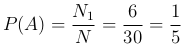
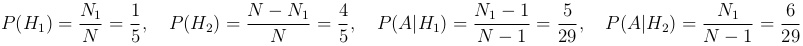
- 1. Студент выбирает билет первым. Тогда
- 2. Студент выбирает билет вторым. Введем гипотезы: H₁ — первый извлеченный билет оказался «счастливым», H₂ — «несчастливым». Тогда
По формуле полной вероятности:

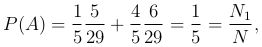
что совпадает с первой ситуацией.
Теорема. Пусть для некоторого события A, P(A)>0, и гипотез H₁, …, H_n известны P(H₁), …, P(H_n) (P(H_i) > 0, i=1,…,n) и P(A|H₁), …, P(A|H_n). Тогда условная вероятность P(H_i|A), i=1,…,n гипотезы H_i при условии события A определяется формулой Байеса:

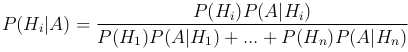
Замечание. Вероятности P(H₁), …, P(H_n) называют априорными (то есть полученными «до опыта»), а условные вероятности P(H₁|A), …, P(H_n|A) — апостериорными (то есть полученными «после опыта»).
Пример. Врач после осмотра больного считает, что возможно одно из двух заболеваний, которое мы зашифруем номерами 1 и 2, причем степень своей уверенности в отношении диагноза он оценивает как 40% и 60% соответственно. Для уточнения диагноза больного направляют на анализ, исход которого дает положительную реакцию при заболевании 1 в 90% случаев и при заболевании 2 — в 20% случаев. Анализ дал положительную реакцию. Как изменится мнение врача после этого?
Обозначим через A — событие, означающее, что анализ дал положительную реакцию. Естественно ввести следующие гипотезы: H₁ — имеет место заболевание 1; H₂ — имеет место заболевание 2. Из условия задачи ясно, что априорные вероятности гипотез равны:
P(H₁) = 0.4; P(H₂) = 0.6,
а условные вероятности события A при наличии гипотез H₁ и H₂:
P(A|H₁) = 0.9 и P(A|H₂) = 0.2.
По формуле Байеса:

Итак, врач с большей уверенностью признает наличие заболевания 1.
Схема Бернулли

Определение. Схемой Бернулли (или последовательностью независимых одинаковых испытаний, или биномиальной схемой испытаний) называют последовательность испытаний, удовлетворяющую следующим условиям:
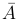- 1) при каждом испытании различают лишь два исхода: появление некоторого события A, называемого «успехом», либо появление его дополнения , называемого «неудачей»;
- 2) испытания являются независимыми, то есть вероятность успеха в k-м испытании не зависит от исхода всех испытаний до k-го;
- 3) вероятность успеха во всех испытаниях постоянна и равна
  P(A)=p.
Вероятность неудачи в каждом испытании обозначим q:

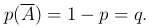
При рассмотрении схемы испытаний Бернулли основной задачей является нахождение вероятности события A_k, состоящего в том, что в n испытаниях успех наступит ровно k раз, k=0, 1, …, n.
Обозначим P(A_k) через P_n(k).
Теорема. Вероятность P_n(k) того, что в n испытаниях по схеме Бернулли произойдет ровно k успехов, определяется формулой Бернулли

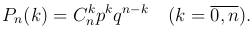
Пример. Монету подбрасывают n=10 раз. Определить вероятность выпадения «герба» ровно 5 раз.

Формула полной вероятности и формула Байеса

Схема Бернулли