Знакопеременные ряды

Определение. Знакопеременным рядом называют ряд с членами имеющими произвольные знаки.

Определение. Если сходится ряд, составленный из своих абсолютных значений:

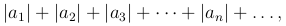(1)

то исходный ряд

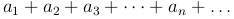(2)

называется абсолютно сходящимся рядом.

Теорема. Из сходимости (1) следует сходимость (2). Причем из расходимости (1) не следует расходимость (2).

□ Пусть

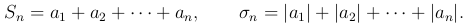
Так как ряд (1) сходится, то

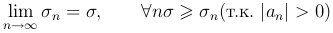(3)

Пусть S_n' - сумма всех положительных членов ряда, а S_n'' - сумма абсолютных величин всех отрицательных членов ряда. Тогда

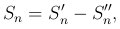(4)

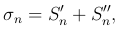(5)

Причем последовательности S_n' и S_n'' неубывающие. Из (3) и (5) следует, что ограничены:

то есть

Тогда из равенства (4)

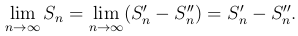
Следовательно, ряд (2) сходится. ■

Определение. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из его модулей, расходится.

Пример. Ряд

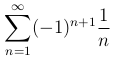
является условно сходящимся.

Замечание. Признаки сходимости для рядов с положительными членами, применимы к знакопеременным рядам, если везде |a_n заменить на a_n|.

Пример. Ряд

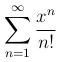
абсолютно сходится при всех конечных значениях x, так как

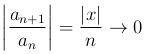
при всех конечных x.

Пример. Ряд

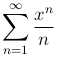
абсолютно сходится при |x| < 1 и расходится при |x| > 1, так как

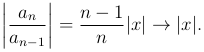
Свойства абсолютно сходящихся рядов

Определение. Перестановка членов абсолютно сходящегося ряда не нарушает его сходимости, сумма ряда при этом остается прежней.

Определение. Абсолютно сходящиеся ряды с суммами S₁ и S₂ можно почленно складывать (вычитать). В результате получится также абсолютно сходящийся ряд с суммой равной S₁ + S₂ (S₁ - S₂).

Определение. Если ряды 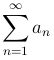и 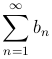сходятся абсолютно, и их суммы равны S₁ и S₂ соответственно, то их произведение

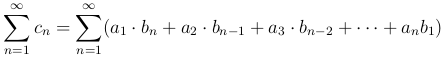
также абсолютно сходится и его сумма равна S₁ · S₂.

Общий признак сходимости

Теорема (общий признак сходимости). Для сходимости бесконечного ряда

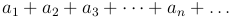
необходимо и достаточно, чтобы для любого заданного положительного ε существовало такое число N, что при всяком n > N и при всяком положительном p выполнялось неравенство

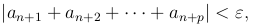
то есть сумма какого угодно числа последовательных членов ряда, начиная с a_n+1, остается по абсолютной величине меньше ε при n > N.

Замечание. Не смотря на теоретическую важность этого общего признака сходимости ряда, применение его на практике обычно затруднительно.