Интегральный признак сходимости Коши

Предположим, что члены ряда

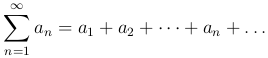
положительны и не возрастают

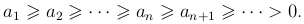
Изобразим члены ряда графически, откладывая по оси абсцисс независимую переменную n, принимающую только целые значения, а по оси ординат - соответствующие значения a_n. Всегда модно найти такую функцию y = f(x), что f(n) = a_n. Причем, будем считать, что функция f(x) не возрастающая.

При таком графическом изображении сумма первых n членов данного ряда

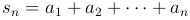
представится как сумма площадей "выходящих" прямоугольников, которая заключает внутри себя площадь фигуры, ограниченной кривой y = f(x), осью Ox и ординатами x = 1 и x = n + 1. По определению интеграла

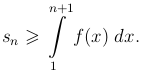
С другой стороны, та же фигура заключает себя все "входящие" прямоугольники, сумма площадей которых равна

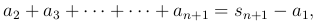
а потому

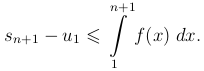
Эти неравенства приводят нас к следующему признаку.

Теорема (Интегральный признак Коши). Ряд 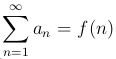члены которого положительны и не возрастают при возрастании n, сходится или расходится с интегралом

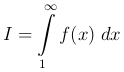
одновременно.

□ Пусть сперва интеграл I имеет конечное значение, то есть кривая y = f(x) имеет конечную площадь. Из положительности f(x) вытекает

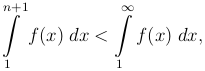
а потому

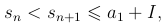
то есть сумма s_n остается ограниченной при всех значениях n следовательно 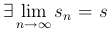и, значит, ряд сходится.

Если I = ∞, то 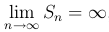, то есть ряд расходится.■

Замечание. При применении признака Коши в интеграле нижний предел, равный единице, можно заменить любым числом a > 1, при этом сходимость или расходимость ряда не изменится.

Пример. Исследуем на сходимость гармонический ряд

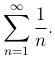
Здесь мы имеем

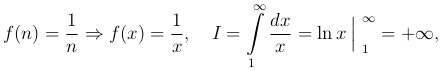
следовательно интеграл (и ряд) расходится.

Пример. Исследуем на сходимость ряд Дирихле:

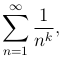
где k - любое число, большее нуля (при k ≤ 0 ряд, очевидно, расходится).

Здесь мы имеем

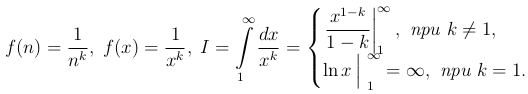
Интеграл расходится, если k ≤ 1, и сходится и равен 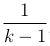, если k > 0.