Признаки сравнения рядов

Теорема (первый признак сравнения рядов). Если каждый член ряда с положительными членами 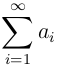(), начиная с некоторого члена n, не превосходит соответствующего члена сходящегося ряда 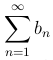(), то ряд () также сходится.

Если же, наоборот, каждый член ряда (), начиная с некоторого n, не меньше соответствующего члена расходящегося ряда () с положительными членами, то и ряд () также расходится.

□ Докажем первое условие: a_n≤b_n и ряд () сходится. Без ограничения общности мы можем считать, что это неравенство выполняется при всех n, отбросив при необходимости первые несколько членов, нарушающих это неравенство. Обозначим через S_n и σ_n частичные суммы первого и второго ряда, соответственно. Из неравенства следует, что S_n≤σ_n, но ряд () сходится и обозначая его сумму через σ получим, что σ_n≤σ и, следовательно, S_n≤σ. В силу конечности σ следует существование конечной суммы ряда и сходимости ряда ().

Для неравенства a_n≥b_n имеем S_n≥σ_n. Из расходимости ряда () следует, что частичная сумма может быть сколь угодно большой, а частичная сумма первого ряда еще больше, следовательно ряд () расходится. ■

Теорема (второй признак сравнения рядов). Если для двух рядов () и () существует конечный и отличный от нуля предел отношения из главных членов

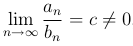
то ряды () и () сходятся и расходятся одновременно.

□ По определению предела последовательности

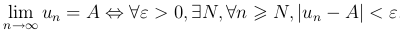
Тогда 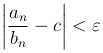или .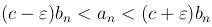

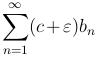Если () сходится, то также сходится и ряд () сходится по первому признаку сравнения.

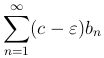Если () расходится, то также расходится и ряд расходится по первому признаку сравнения.■