Признаки сходимости рядов

Теорема (Признак Коши). Если общий член ряда с положительными членами 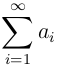начиная с некоторого значения n, удовлетворяет неравенству

()

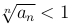то ряд сходится, если же

()

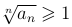то расходится.

□ Без ограничения общности, можем считать, что неравенства (), () выполняются при всех значениях n. Если выполняется (), то a_n < qⁿ, т.е. общий член данного ряда не превосходит соответствующего члена бесконечно убывающей геометрической последовательности, следовательно, по первому признаку сравнения, ряд будет сходящимся. В случае () имеем a_n ≥ 1 - общий член ряда не стремится к нулю (больше 1) и, значит, не выполняется необходимый признак сходимости и ряд будет расходящимся. ■

Теорема (Признак Даламбера). Если отношение последующего члена ряда к предыдущему a_n/a_n-1, начиная с некоторого n, удовлетворяет неравенству

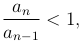
то ряд сходится, в противном случае

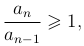
расходится.

□ Без ограничения общности, можем считать, что неравенства (), () выполняются при всех значениях n, тогда

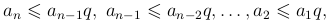
откуда, перемножая почленно и сокращая общие множители

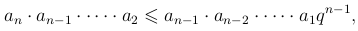
получаем

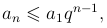
то есть члены ряда меньше членов убывающей геометрической прогрессии, следовательно, по первому признаку сравнения ряд сходится. В случае () - члены ряда не убывают по мере удаления от начала, следовательно a_n не стремиться к нулю при n → ∞ и ряд является расходящимся по необходимому признаку сходимости. ■

Следствие. Если

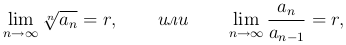
то ряд 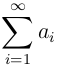сходится при условии r < 1 и расходится при r gt; 1.

□ Пусть сперва r < 1. Выберем число ε настолько малым, чтобы было также и r + ε < 1. При больших значениях n величина 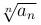или 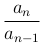будет отличаться от своего предела r не больше, чем на ε, т.е. мы, начиная с некоторого достаточно большого значения n будем иметь

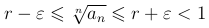
или

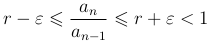
Применяя признак Коши или Даламбера при q = r + ε < 1, получаем сходимость ряда.

Аналогичным образом доказывается и расходимость ряда при r > 1. ■

Пример. Исследуем на сходимость ряд

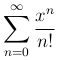
Применяя признак Даламбера

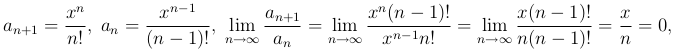
следовательно ряд сходится при всех положительных конечных значениях x.

Пример. Исследуем на сходимость ряд

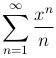
Здесь мы имеем

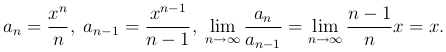
По признаку Даламбера ряд сходится при$0 ≤ x < 1 и расходится при x > 1.

Пример. Исследуем на сходимость ряд

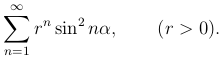
Применяя признак Коши, имеем

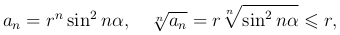
Следовательно ряд сходится при r < 1.

Признак Даламбера в данном случае не дает никакого резльтата, ибо отношение

не стремится ни к какому пределу и даже не остается все время < 1 или ≥ 1.

Замечание. Признак Коши сильнее признака Даламбера, т.е. он может применяться во всех случаях, когда применяется признак Даламбера, ео сверх того и в некоторых других, когда последний не может применяться. Однако признак Коши более сложен в использовании, чем признак Даламбера.

Замечание. В случаях, когда

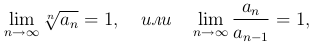
то есть, когда r = 1, признак Коши и Даламбера не могут применяться, и в этом случае вопрос о сходимости или расходимости должен решаться другими способами.

Пример. Продемонстрируем это на примере гармонического ряда (ряд расходится)

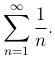
Признак Даламбера дает:

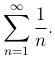
Признак Коши дает:

Пример. Рассмотрим еще один (сходящийся, как мы увидем дальше) ряд

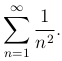
Признаки Даламбера и Коши дают

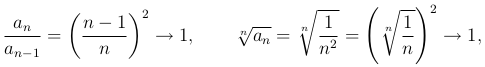
То есть информации о сходимости этого ряда эти признаки дать не могут.