Ряды
Комплексная форма рядов Фурье
Ряд Фурье
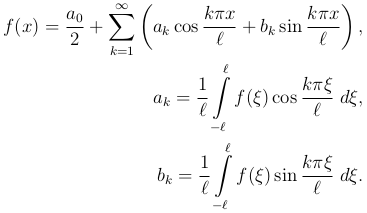(1
)
можно представить в комплексной форме:
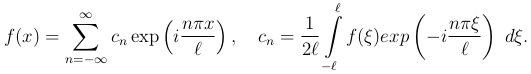(2)
Здесь индекс n принимает не только целые положительные, но и отрицательные значения. Определим отдельно c0, ck и c-k, где k - целое положительное число. Согласно (1) и (2) имеем
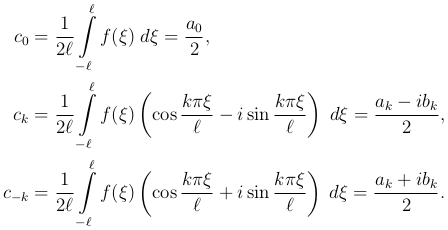
Подставляя в ряд (2) и суммируя отдельно по положительным и отрицательным индексам, получим
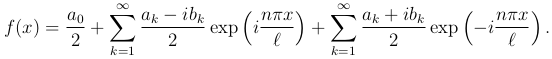
Слагаемые двух написанных сумм при одинаковых k суть мнимые сопряженные величины. Соединяя их в одно слагаемое, получим вещественную величину
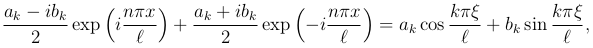
и предыдущее выражение для f(x) совпадает с рядом Фурье (1), откуда и следует равносильность (1) и (2).