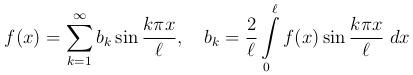Ряды
Ряды
 Ряд Фурье для четных и нечетных функций
Ряд Фурье для четных и нечетных функций
При вычислении коэффициентов Фурье часто бывает полезно пользоваться следующей леммой: \begin{Lemma}
Лемма. Если f(x) есть четная функция в промежутке (-a, a), то есть f(-x) = f(x), то
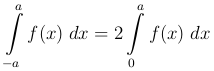
и если f(x) - нечетная функция, то есть f(-x) = - f(x), то
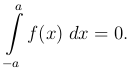
Таким образом, для четной функции f(x) имеем
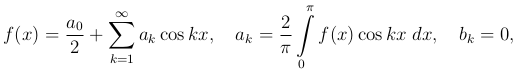 (1
(1 )
)
а для нечетной функции f(x)
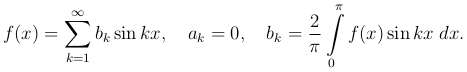 (2
(2 )
)
Пусть теперь нам дана произвольная функция f(x), определенная в промежутке (0, π). Эту функцию можно разложить в промежутке (0, π) как в ряд вида (1 ), содержащий только косинусы, так и в ряд вида (2
), содержащий только косинусы, так и в ряд вида (2 ), содержащий только синусы. Оба эти ряда внутри промежутка (0, π) будут иметь суммой функцию f(x) или среднее арифметическое в точках разрыва. Но вне промежутка (0, π) они будут представлять совершенно различные функции: ряд по косинусам даст функцию, получающуюся из f(x) четным продолжением в соседний промежуток (-\pi, 0), а затем периодическим продолжением с периодом 2π вне промежутка (-π, π). Ряд по синусам дает функцию, получающуюся нечетным продолжением функции f(x) в соседний промежуток (-\pi, 0) и затем периодическим продолжением с периодом 2π вне промежутка (-π, π).
), содержащий только синусы. Оба эти ряда внутри промежутка (0, π) будут иметь суммой функцию f(x) или среднее арифметическое в точках разрыва. Но вне промежутка (0, π) они будут представлять совершенно различные функции: ряд по косинусам даст функцию, получающуюся из f(x) четным продолжением в соседний промежуток (-\pi, 0), а затем периодическим продолжением с периодом 2π вне промежутка (-π, π). Ряд по синусам дает функцию, получающуюся нечетным продолжением функции f(x) в соседний промежуток (-\pi, 0) и затем периодическим продолжением с периодом 2π вне промежутка (-π, π).
Таким образом, при разложении по косинусам
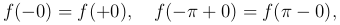
а при разложении по синусам
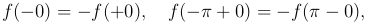
Часто бывает нужно разлагать в тригонометрический ряд по косинусам и синусам функцию f(x), определяемую не в промежутке (-π, π), а в промежутке (-l, l), или же в ряд только по косинусам или только по синусам функцию, определенную в промежутке (0, l). Эта задача приводится к предыдущей с помощью изменения масштаба, т.е. введения вместо x вспомогательной переменной ξ по формуле
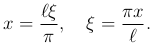 (3
(3 )
)
Положим
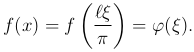
Если функция f(x) была определена в промежутке (-l, l), то функция φ(ξ) будет определена в промежутке (-π, π) переменной ξ. Разлагая функцию φ(ξ) в ряд Фурье, получаем
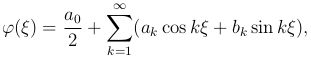
где, в силу (3 )
)
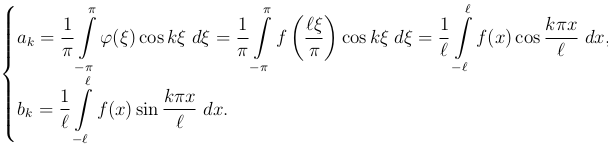 (4
(4 )
)
Таким образом теорема Дирихле остается верной и для промежутка (-l, l) с тем, однако, что разложение ( ) заменяется разложением
) заменяется разложением
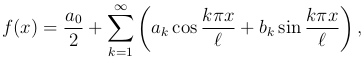
причем коэффициенты ak и bk определяются по формулам (4 ).
).
Тоже относится и к разложениям функции f(x), определенной в промежутке (0, l), только по косинусам или только по синусам; для функции f(x) получаются ряды
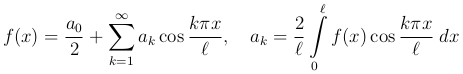 и
и