Ряды
Сходимость функциональных последовательностей и рядов
Ряд, составленный из функций f(xn), является функциональным рядом.
Рассмотрим последовательность функций
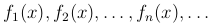
Зафиксировав x=x0, получим числовую последовательность
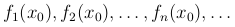
Определение. Функциональная последовательность {fn(x)} называется сходящейся в точке x0, если сходится соответствующая числовая последовательность {fn(x0)}.
Определение. Последовательность {fn(x)} называется сходящейся к функции f(x) на множестве X, если для всех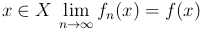 
.
Последнее равенство означает следующее: для каждого x ∈ X и любого ε > 0 существует номер N=N(ε, x): для любого n > N выполняется равенство |f(x) - fn(x)| < ε.
Пусть дан функциональный ряд
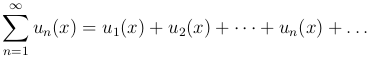
Зафиксируем некоторое значение x=x0, получим числовой ряд
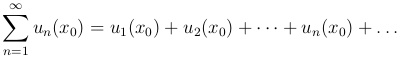
Определение. Если числовой ряд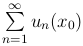 
сходится, то значение x0 называется точкой сходимости функционального ряды 
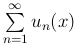. Множество всех точек сходимости функционального ряда называется областью его сходимости. Если числовой ряд 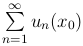расходится, то x0 называется точкой расходимости функционального ряда .
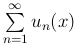Определение. Функциональный ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Определение. Функциональный ряд называется абсолютно сходящимся на множестве X, если на нем сходится ряд из модулей его членов:
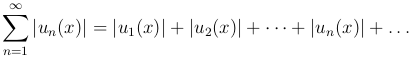
Поскольку каждой точке x0 сходимости ряда
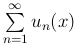ставится в соответствие определенное значение суммы ряда 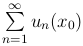, то сумма сходящегося на множестве X функционального ряда является функций переменной x. Обозначим эту функцию через
S(x), тогда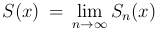 
, где Sn(x) - n-я частичная сумма ряда 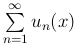, то есть Sn(x) = u1(x) + u2(x) + … + un(x).
Определение. Остатком функционального ряда 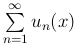после его n-го члена (или n-м остатком) называется ряд, полученный из данного отбрасыванием n его первых членов, то есть
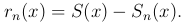
Утверждение. Функциональный ряд 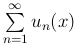и любой его остаток на множестве X одновременно сходится или расходится.
Замечание. Каждому функциональному ряду
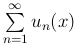можно поставить в соответствие функциональную последовательность, а именно, последовательность
его частичных сумм:
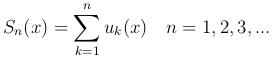
С другой стороны, каждой функциональной последовательности {fn(x)} соответствует функциональный ряд f1(x)+[f2(x)-f1(x)]+…+[fn(x)-fn-1(x)]+… для которого частичные суммы будут равны соответствующим членам последовательности {fn(x)}, то есть Sn(x)=fn(x).
Это дает возможность каждую теорему, доказанную для функциональных рядов, перефразировать в соответствующую теорему для функциональных последовательностей, и наоборот.