Интеграл Фурье

Исследуем предельный случай, когда промежуток (-l, l) стремиться к (-∞, ∞), то есть l → ∞.

Пусть функция f(x) удовлетворяет условиям Дирихле и непрерывна во всяком конечном промежутке и сверх того абсолютно интегрируема в промежутке (-∞, ∞), то есть существует интеграл

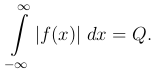
По теореме Дирихле внутри (-l, l) мы имеем

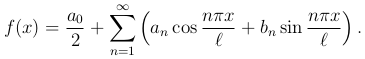
Помня, что

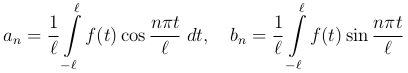
мы получим отсюда

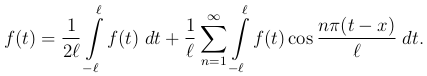
Что произойдет с этой формулой, когда l → ∞? Первое слагаемое очевидно стремится к нулю, ибо

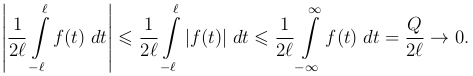
Вводя новую переменную α, которая принимает равноотстоящие начения в промежутке (0, ∞):

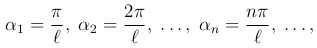
получая каждый раз приращения Δ α = π/l, мы оставшуюся сумму можем написать в виде

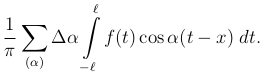
При больших l интеграл, стоящий под знаком суммы, мало отличается от

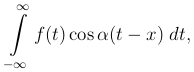
и можно полагать, что вся сумма при l → ∞ будет стремиться к пределу

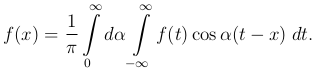
В точках разрыва непрерывности, если таковые имеются, надо только заменить f(x) на

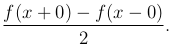
Формула эта, которая получается из ряда Фурье при l → ∞, называется формулой Фурье. Мы приходим таким образом к предложению: если функция f(x) удовлетворяет условиям Дирихле во всяком конечном промежутке и абсолютно интегрируема в промежутке (-∞, ∞), то при всех x имеет место равенство

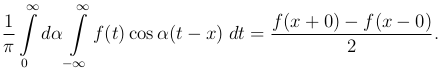(1)

Теорема эта называется обычно теоремой Фурье, а интеграл, стоящий в левой части этой формулы, интегралом Фурье функции f(x).

Формула (1) может быть преобразована, если функция f(x) четная или нечетная. В самом деле, раскрывая cos α (t - x) имеем

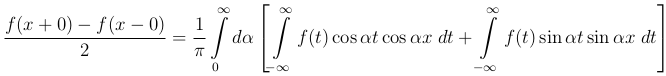(2)

причем оба интеграла по t имеют, очевидно, смысл в виду абсолютной интегрируемости f(t) в промежутке (-∞, ∞).

Если функция f(t) - четная, то функция f(t) cos α t - четная, а функция f(t) sin α t -нечетная, и, следовательно,

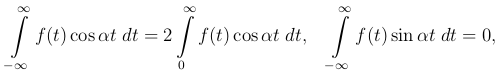
так что

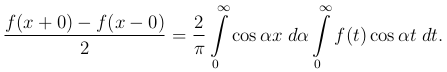
Если же функция f(x) - нечетная, то таким же образом получим

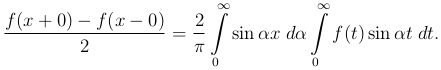
Если функция f(x) определена только в промежутке (0, ∞), ее можно продолжить в соседний промежуток (-∞, 0) четным или нечетным образом и тогда мы для одной и той же функции f(x), считая ее для простоты непрерывной, получим две формулы

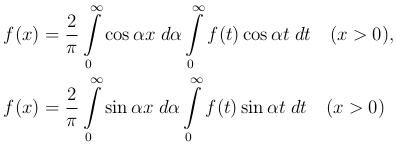(3)

Нужно только помнить, что для первой из них функция f(x), продолжаясь четно, дает непрерывную функцию от x, так что первая формула верна и при x = 0; во второй же формуле, если f(x) ≠ 0, мы получим разрыв, и правая часть при x = 0 равняется не f(0), а нулю.

Преобразование Фурье

В формуле (2) первое интегрирование совершается по t, и, введя две функции

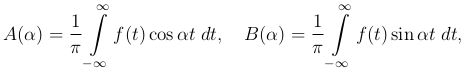
мы можем переписать формулу (2) в виде

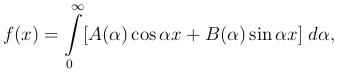
считая для простоты f(x) непрерывной. В этой формуле мы имеем разложение f(x) в бесконечном промежутке (-∞, ∞) на гармонические колебания, причем частоты α этих колебаний непрерывно меняются от 0 до ∞, а функции A(α) и B(α) дают закон распределения амплитуд и начальных фаз в зависимости от частоты α. Для конечного промежутка (-l, l мы имели частоты α_n = nπ/l, (n = 0, 1, …), образующие арифметическую прогрессию.

Если в первой формуле (3) положить

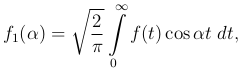(4)

то ее можно переписать в виде

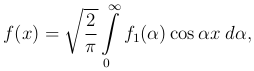(5)

В этих двух формулах f(x) и f₁(α) совершенно одинаково выражаются одна через другую.

Если считать в формуле (5) f(x) заданной и f₁(α) - искомой, то формула (5) представляет собою так называемое интегральное уравнение для f₁(α), поскольку эта функция входит под знак интеграла (интегральное уравнение Фурье). Формула (4) дает решение этого интегрального уравнения. Совершенно также вторую формулу (3) мы можем представить в виде следующих формул: