Знакочередующиеся ряды

Определение. Знакочередующимся рядом называется ряд, в котором любые два последовательных члена отличаются знаком:

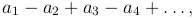
причем числа a_i считаются положительными.

Теорема (Признак Лейбница). Для того, чтобы знакопеременный ряд сходился, достаточно, чтобы абсолютные значения его членов убывали и стремились к нулю при возрастании n. Остаток такого ряда по абсолютной величине не превосходит абсолютного значения первого из отброшенных членов.

□ Рассмотрим суммы четного числа членов ряда

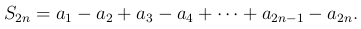
Так как абсолютные значения членов ряда убывают при возрастании n, то

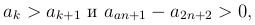
а потому

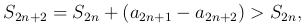
то есть частичная сумма S_2n - не убывающая. С другой стороны, мы имеем

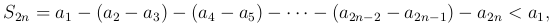
так как все разности в скобках неотрицательны, т.е. сумма S_2n остается ограниченной при всех значениях n. Отсюда следует, что при возрастании n, S_2n стремится к конечному пределу S:

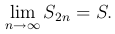
Далее мы имеем

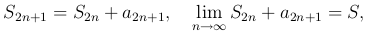
так как по условию

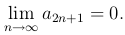
Таким образом, сумма четного и сумма нечетного числа членов ряда стремиться к одному и тому же пределу S, т.е. ряд сходящийся и имеет сумму S.

Оценим остаток R_n ряда:

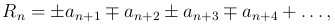
причем одновременно нужно врать либо верхние, либо нижние знаки, то есть

()

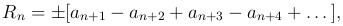откуда, рассуждая как и раньше, имеем

■

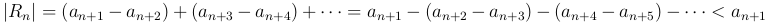Из формулы () следует, что знак R_n совпадает с тем знаком, который нужно брать перед квадратной скобкой, т.е совпадает со знаком ± a_n+1. Итак, в указанных в теореме условиях знак остатка знакочередующегося ряда совпадает со знаком первого из отброшенных членов.

Пример. Исследуем ряд

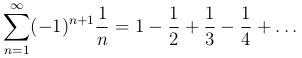
Члены ряда убывают при возрастании n и модуль общего члена ряда стремится к нулю при n → ∞:

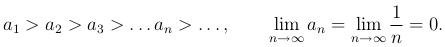
Следовательно, ряд сходящийся (как мы увидим в дальнейшем к значению ln 2). Отметим, что данных ряд хоть и сходится, но сходится очень медленно.