Ряды
Ряды
Введем основные понятия и определения, связанные с числовыми рядами.
Определение 1. Пусть задана бесконечная числовая последовательность a1, a2, ⋯, an, ⋯. Числовым рядом называется выражение вида
Сокращенно ряд обозначают следующим образом:
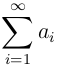
Числа ai называются членами ряда, а число an - общим членом ряда.
Определение 2. Сумма конечного числа n первых членов ряда
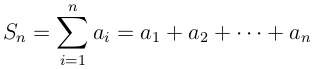
называется частичной суммой ряда.
Определение 3. Если частичная сумма Sn имеет конечный предел при n → ∞
,
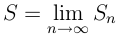то S называют суммой ряда, а ряд называется сходящимся.
Замечание. Если предел частичной суммы не существует или равен бесконечности, то ряд называется расходящимся и суммы ряда не существует.
Частичная сумма сходящегося ряда является приближенным выражением для суммы ряда, а его погрешность Rn=S-Sn называется остатком ряда.
Свойство 1. Если ряд
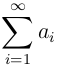сходится и имеет сумму S, то ряд 
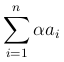, получаемый из предыдущего умножением всех членов ряда на одно и то же число α также сходится и имеет сумму αS.
□
■
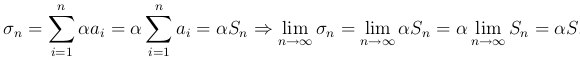Свойство 2. Сходящиеся ряды можно почленно складывать и вычитать. То есть, если
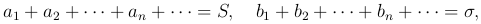
то ряд
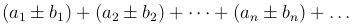
также сходится и его сумма равна S±σ.
□ Сумма первых членов ряда
■
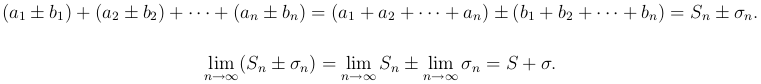Свойство 3. Сходимость и расходимость ряда не нарушается, если в ряде отбросить или приписать к нему любое конечное число членов с начала.
□ Рассмотрим два ряда (во втором отброшено первые k членов):
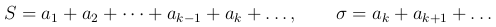
Очевидно, что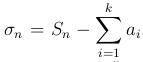 
. При n→∞ частичные суммы имеют предел, так как с правой стороны стоит сходящийся ряд плюс константа и, следовательно, слева предел ряда конечен и равен
■
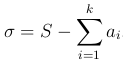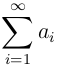сходится, то
. (
)
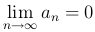□ Если ряд сходится и имеет сумму S, то
■
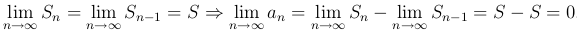Замечание. Условие () необходимо для сходимости ряда, но оно не достаточно: общий член ряда может стремиться к нулю, и все же ряд будет расходящимся.
Замечание. Если условие () не выполняется, то ряд расходится.