Ортогональность тригонометрических функций

Рассмотрим периодическую функцию с периодом 2π: 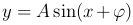. Мы можем выбрать более сложные функции того же типа

Определение. Тригонометрическим полиномом n-го порядка называется сумма

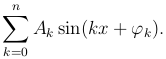
Мы можем приближенно представить произвольную функцию f(x) в виде тригонометрического полинома n-го порядка

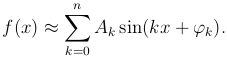
Рассмотрим вопрос о разложениее функции f(x) в тригонометрический ряд

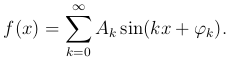
Определение. Общий член тринонометрического ряда 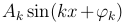называется k-й гармоникой функции f(x).

Мы можем записать

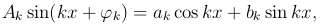
где

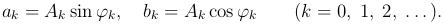
Гармоника нулевого порядка A₀ sin φ₀ есть просто постоянная, которую мы для упрощения дальнейших формул обозначим через a₀/2. Итак, наша задача заключается в том, чтобы подобрать, если возможно, неизвестные постоянные

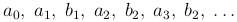
так, чтобы ряд

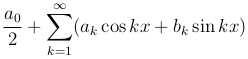(1)

был сходящимся и чтобы его сумма равнялась заданной периодической функции f(x) периода 2 π.

Для решения этого вопроса выясним одно простое свойство косинусов и синусов кратных дуг. Пусть c - любое вещественное число и (c, c + 2 π) - любой промежуток длины 2π. Нетрудно доказать, что

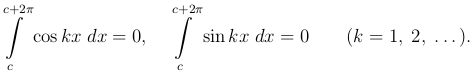(2)

Рассмотрим, например, первый из написанных интегралов. Первообразная функция для cos kx равна k^-1 sin kx и, ввиду ее периодичности, ее значения при x = c и x = c + 2π будут одинаковы, и разность этих значений будет нуль, т.е., действительно,

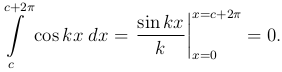
Совершенно также, пользуясь известными формулами тригонометрии:

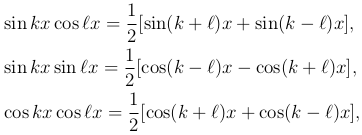
можно доказать, что

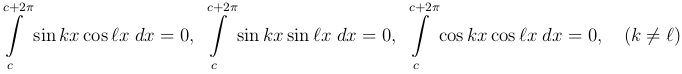(3)

Рассмотрим семейство функций

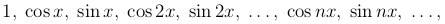(4)

причем первой из функций семейства является постоянная, равная единице. Формулы (2) и (3) выражают следующий факт: интеграл от произведения любых двух различных функций семейства (4) по любому промежутку длины$2 π равен нулю. Такое свойство называется обычно свойством ортогональности семейства (4) на указанном промежутке. Вычислим теперь интеграл от квадрата функций семейства (4). Для первой из функций этот интеграл равен очевидно 2 π, а для остальных, в силу формул

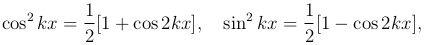
мы будем иметь

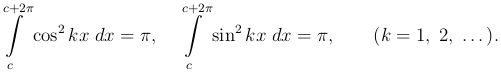
В дальнейшем для определенности мы будем брать c = -π, т.е. роль промежутка (c, c + 2π) будет у нас играть промежуток (-π, π).