Степенной ряд

Определение. Степенным рядом называется функциональный ряд вида

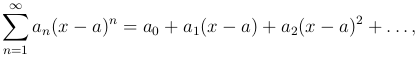
где a_n (n = 0, 1, 2, …) - постоянные, называемые коэффициентами ряда.

При a = 0 степенной ряд принимает вид .

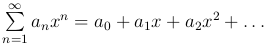Теорема (Первая теорема Абеля). Если степенной ряд 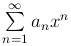сходится при некотором значении x = x₀ ≠ 0, то он абсолютно сходится при любом x, для которого |x| < |x₀|.

□ Пусть сперва ряд

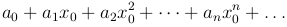
сходится, тогда общий член сходящегося ряда должен стремиться к нулю, т.е.

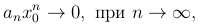
а потому можно найти такую постоянную M, чтобы при всех значениях n мы имели

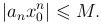
Придадим теперь x любое значение, удовлетворяющее условию |x| < |x₀|, и положим

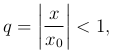
Мы имеем

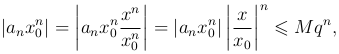
то есть общий член ряда при рассматриваемом значении x по абсолютной величине не привосходит общего члена убывающей геометрической прогрессии, а потому ряд сходится абсолютно. ■

Следствие 1. Если степенной ряд расходится при некотором значении x₁, то он расходится и при любом x, для которого |x| > |x₁|.

Следствие 2. Если степенной ряд сходится при x₀ ≠ 0, то он сходится при любом x из интервала (-|x₀|,|x₀|); если расходится при x = x₁, то расходится вне интервала (-|x₁|, |x₁|), то есть при x < |x₁| и x > |x₁|.

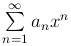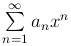Определение. Радиусом сходимости степенного ряда называется число R такое, что при |x| < R ряд сходится, а при |x| > R расходится. Интервалом сходимости ряда называется интервал (-R, R), где R - радиус сходимости.

На концах интервала сходимости ряд может сходиться или расходиться. Если степенной ряд сходится на всей числовой оси, то полагают R = ∞. Если он сходится только при x = 0, считают R = 0.

Замечание. Аналогично определяются радиус и интервал сходимости ряда 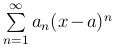: если при |x-a| < R этот ряд сходится, а при |x-a| > R расходится, то R - радиус его сходимости, (a-R, a+R) - интервал сходимости.

Выражения для радиуса сходимости степенного ряда 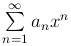через его коэффициенты:

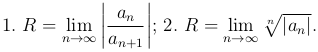
Теорема (Вторая теорема Абеля). Если R есть радиус сходимости ряда, то ряд сходится не только абсолютно, но и равномерно в любом промежутке (a, b), лежащим целиком внутри промежутка (-R, +R), то есть для которого -R < a < b < R. Если же ряд сходится и при x = R или x = -R, то он будет равномерно сходящимся и в промежутке (a, R) или (-R, b).

Следствие 1. Сумма степенного ряда является непрерывной функцией на любом отрезке, целиком принадлежащем его интервалу сходимости.

Следствие 2. Степенной ряд можно почленно интегрировать по любому отрезку [α, β], целиком принадлежащему его интервалу сходимости (-R, R).

Теорема. Если степенной ряд 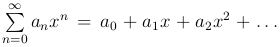имеет интервал сходимости (-R, R) и S(x) - его сумма, то ряд 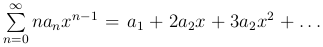полученный почленным дифференцированием ряда 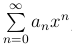, имеет тот же интервал сходимости, причем

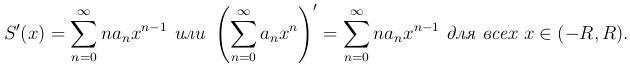
Следствие. Степенной ряд можно почленно дифференцировать любое число раз в интервале его сходимости.