Разложение элементарных функций в степенной ряд

Экспоненциальная функция имеет следующее разложение в ряд Тейлора:

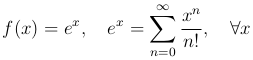
В частности, основание натурального логарифма равно

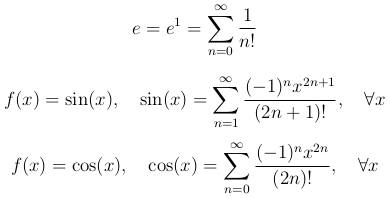
Бином Ньютона .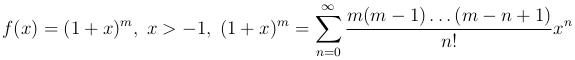

В случае log(x) разложение по формуле Тейлора по степеням x не применимо, так как при x = 0 она сама и ее производные терпят разрыв непрерывности и обращаются в бесконечность. Мы можем найти выражение для log(1+x).

Покажем, что ()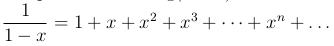

Ряд 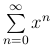сходится при |x| < 1 и представляет собой геометрическую прогрессию со знаменателем q = x. Сумма его вычисляется по формуле 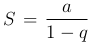, 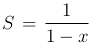(a=1, q=x). Следовательно, формула () представляет собой разложение функции 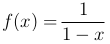в степенной ряд; радиус сходимости R = 1.

Записав в последнем равенстве (-t) вместо x, получим разложение в степенной ряд функции 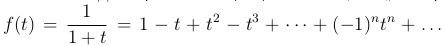Это равенство можно получить непосредственно, поскольку ряд 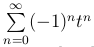сходится при |t| < 1 и его сумма равна .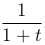

Интегрируя последний ряд по отрезку [0,x], где |x| < 1, получим

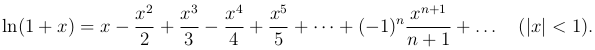
Этот ряд сходится при |x| < 1, поскольку степенной ряд сходится на любом отрезке, целиком принадлежащем его интервалу сходимости. При x = 1 ряд также сходится (из рассмотренного ранее примера), при x = -1 ряд расходится (получен из гармонического ряда умножением на (-1)). Следовательно, ряд 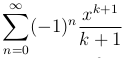сходится при -1 < x ≤ 1.

Можем получить также следующий ряд 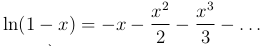и ряд вида:

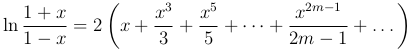
Это разложение имеет место при |x| < 1.