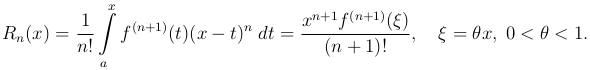Формула Тейлора

Рассмотрим многочлен n-й степени:

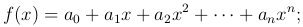
придадим приращение h и вычислим соответствующее значение функции f(x+h). Это значение, очевидно, можно разложить по степеням h, раскрывая различные степени x+h по формуле бином Ньютона и рсполагая окончательный результат по степеням h. Коэффициенты при различных степенях h будут многочленами, зависящими от x:

()

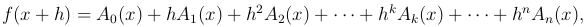и нужно только определить многочлены:

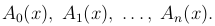
Для этого мы изменим обозначения, написав в тождестве () a вместо x и x вместо x+h. Тогда, h = x - a, и, вместо (), мы получим

()

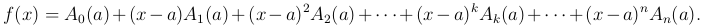Для определения A₀(a) положим в этом тождестве x = a, что даст f(a) = A₀(a).

Для определения A₁(a) продифференцируем тождество () по x и затем положим x = a:

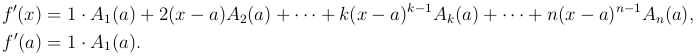
Дифференцируя еще раз по x и полагая затем x = a, получим

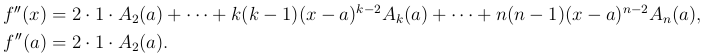
Продолжая эти операции, дифференцируя k раз по x и затем полагая x = a, получим

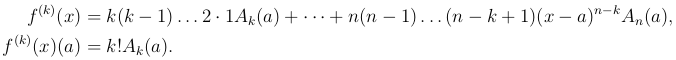
Итак, мы имеем

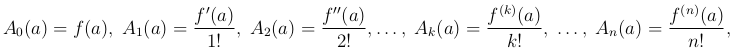
после чего формула () примет вид

()

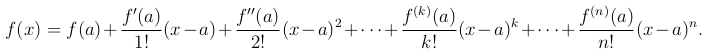Эта формула верна только в том случае, когда f(x) есть многочлен степени не выше n, и она дает разложение такого многочлена по степеням разности (x-a).

Положим теперь, что f(x) - не многочлен, а какая-либо функция, определенная внутри некоторого промежутка I и имеющая непрерывные производные до порядка (n+1). Пусть значение x=a находится внутри I. В дальнейшем считаем, что x принадлежит I.

Обозначим через R_n(x) разность между f(x) и правой частью формулы (), то есть положим

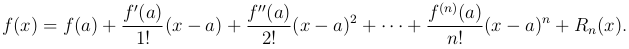(2)

Дифференцируем последовательно это тождество:

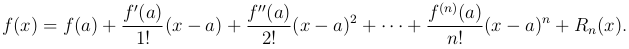(3)

Полагая в (2) и (3) x = a, получаем

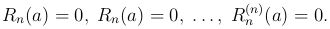(4)

Дифференцируя последнее из равенств (3) еще один раз, найдем

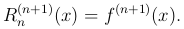(5)

Из соотношений (4) и (5) мы без труда получим выражение для R_n(x), ибо по основной формуле интегрального исчисления

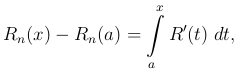
откуда, принимая во внимание (5) и интегрируя по частям, выводим последовательно

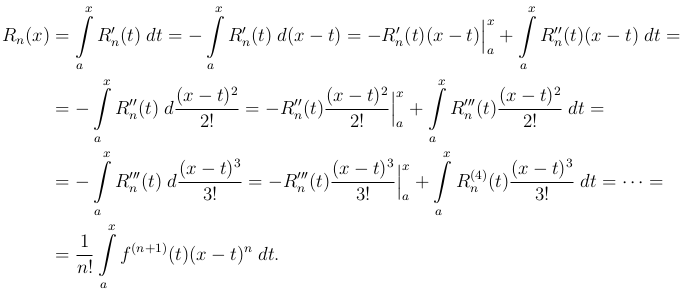
Для уяснения сделанных преобразований заметим следующее. Переменная интегрирования обозначена буквой t, так что x под знаком интеграла надо считать постоянным и дифференциал x равным нулю, и потому,

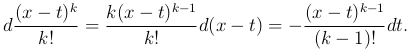
Точно также выражение

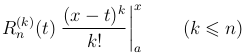
обращается в нуль, так как приподстановке t = x обращается в нуль множитель (x-t)^k, а при подстановке t=a множитель R_n^(k)(a) в силу (5).

Теорема (формула Тейлора). Всякая функция f(x), имеющая внутри некоторого промежутка, содержащего точку x=a внутри себя, непрерывные производные до (n+1)-го порядка включительно, при всех значениях хвнутри этого промежутка может быть разложена по степеням разности (x-a) в виде

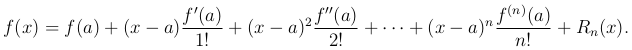
где R_n(x), остаточный член формулы, имеет вид

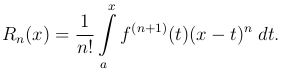(6)

Весьма часто в приложениях встречается другая форма остаточного члена, которая непосредственно получается из (6) при применении теоремы о среднем. Под знаком интеграла в правой части формулы (6) функция (x-t)ⁿ сохраняет знак, а потому по теореме о среднем мы имеем

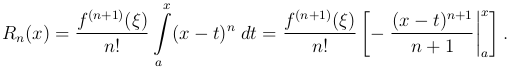
Подставляя верхний и нижний пределы, получим

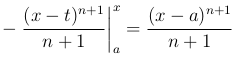
так как при t = x написанное выражение обращается в нуль. Подставляя это в предыдущую формулу, будем иметь

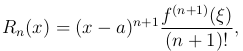
где ξ есть некоторое среднее значение, лежащее между a и x. Эта форма остаточного члена называется остаточным членом в форме Лагранжа, и формула Тейлора состаточным членом Лагранжа будет

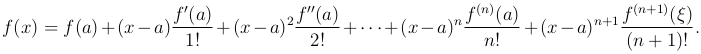
Определение (Формула Маклорена). Если положить в формуле Тейлора a = 0, то получим формулу Маклорена:

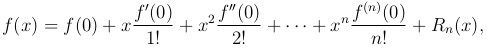
где