Ряды Тейлора и Маклорена

Если f(x) имеет при x=a и x близких к a производные всех порядков, то мы можем написать формулу Тейлора при любом значении n. Перепишем формулу Тейлора в виде:

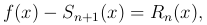
где

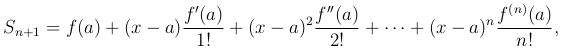
то есть S_n+1(x) есть сумма первых (n+1) членов бесконечного ряда

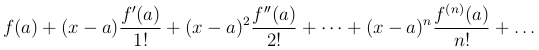
Если при некотором значении x и беспредельном возрастании n

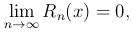
то, указанный выше бесконечный ряд сходится при указанном значении x и его сумма равна f(x). Таким образом, получается разложение функции f(x) в бесконечный степенной ряд Тейлора:

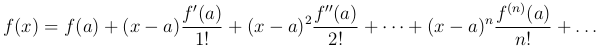
по степеням (x-a).

Ряд Маклорена получается при a = 0:

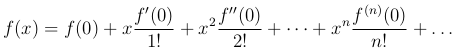
Теорема [Необходимое и достаточное условие сходимости к функции f(x) ее ряда Тейлора]. Ряд Тейлора сходится к f(x) тогда и только тогда, когда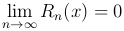

Теорема. Если при любых x, удовлетворяющих неравенству |x-a| < R, производные функции f(x) всех порядков ограничены одним и тем же числом C > 0, то есть

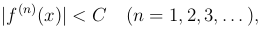
то ряд Тейлора для этой функции сходится в интервале (a-R, a+R) и его сумма равна f(x).

Аналогичные теоремы мы можем получить для ряда Маклорена положив a = 0.